Making Observations: The Ergodic Hypothesis

Scientists are taught early on that when conducting measurements, one must perform repeated experiments and average the results. If one makes $\mathscr{N}$ independent measurements of some observable $G$, one computes the mean value as

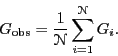$$G_{\rm obs} = \frac{1}{\mathscr{N}}\sum_{i=1}^{\mathscr{N}}G_i.$$ (6)

We now imagine that the time of a measurement is so short that we know that the system is in only one of its many possible microstates. This means we can write

$$G_{\rm obs} = \sum_{\nu}\left[\frac{1}{\mathscr{N}}\left(\be... ... $\mathscr{N}$ observations} \end{array}\right)\right]G_\nu,$$ (7)

where $G_\nu$ was introduced previously (Eq. 1) as the value of observable $G$ when the system is in state $\nu$.

Now we have to imagine that our system is evolving in time. As it evolves, its degrees of freedom change values, and the system is thought of as tracing out a trajectory in state space. (``State space'' is a Hilbert space spanned by all states $\left\vert\nu\right>$ in the quantum mechanical case, or phase space in the classical case.) How is the system evolving? The system wavefunction evolves according to Schrödinger's equation, while particles in a classical system follow Newtonian mechanics. (We will consider Newtonian mechanics in much greater detail later in Sec. 4.) As the experimenters, we control the system by specifying a handful of variables, such as its total energy, $E$, the number of particles, $N$, and the volume, $V$. These contraints force the system's trajectory to remain on a hyperdimensional surface in state space.

The key assumption we make at this point is that, if we wait long enough, our system will visit every possible state; that is, the trajectory will eventually pass through every available point in state space consistent with our constraints. If this is true, and we make $\mathscr{N}$ independent observations, then the number of times we observe the system in state $\nu$ divided by the number of observations, $\mathscr{N}$, is the probability of observing state $\nu$, $P_\nu$, if we happen to make a random observation. So, Eq. 7 above becomes the ensemble average first presented in Eq. 1:

$$G_{\rm obs} = \sum_\nu P_\nu G_\nu = \left<G\right>$$ (8)

We see that a time average is the same as an ensemble average.

This assumption is important: it is referred to as the ergodic hypothesis. A system is ``ergodic'' if, after a sufficiently long time, it visits all possible state space points consistent with whatever constraints are put on it. We cannot in general prove that any system is ergodic; it is something we are comfortable assuming for most systems based on our physical intuition. There are, however, many systems which are non-ergodic. For the most part, we will not concern ourselves with such systems in this course.

Another important consideration is the following: How far apart must the $\mathscr{N}$ independent measurements be from one another in time to be considered truly ``independent''? To answer this question, we must introduce the notion of a relaxation time, $\tau_{\rm relax}$, which arises naturally due to the presumably chaotic nature of the microscopic system. Given some initial conditions, after a time $\tau_{\rm relax}$ has elapsed, the system has ``lost memory'' of the initial condition. We measure this loss of memory in terms of correlation functions, which will be discussed in more detail later. If we wait at least $\tau_{\rm relax}$ between successive observations, we know they are independent. It turns out that one can use simulation methods to estimate relaxation times (and their spectra; many systems display a broad spectrum of relaxation times, each element cooresponding to a particular type of molecular motion). We will pay particularly close attention to $\tau_{\rm relax}$ in upcoming sections.