Bounding the Region of Entropic Vectors
Characterizing the set of entropic vectors under various distribution constraints is a fundamentally important problem in information theory and network coding [B1, B2]. Not only would such an accurate characterization allow for the determination of all information inequalities, but it would enable the direct computation of all rate regions for network coding and multiterminal source coding. That is, understanding the fundamental limits for communication over networks is inherently linked with understanding the boundary of the set of entropic vectors.
The interest in the (closure of) the set of entropic vectors for discrete unbounded cardinality random variables N* [B1] and its normalized counterpart N* [B2, B3] originated in the study of linear information inequalities [B4, B5, B6] and conditional independence structure representations [B7, B8, B9]. More recently, it has been noted that the network coding capacity region [B1, B10] is a linear projection of N* intersected with a vector subspace. These two problems are inherently related, as it has been shown [B11] that for every non-Shannon type inequality (i.e., every supporting half space of N*) there is a multi-source network coding problem for which the capacity region requires this inequality.
More generally, as all achievable rate regions in information theory are expressed
in terms of information measures between random variables obeying certain
distribution constraints, they can be expressed as linear projections of entropic
vectors associated with these constrained random variables. Hence, there is a
fundamental interest in multi-terminal information theory in the region of entropic
vectors N*( ) associated with random variables obeying distribution constraints
) associated with random variables obeying distribution constraints
 .
.
In this project, we develop approaches that bound the region of entropic vectors, which include determining the entropic region for binary discrete random variables, matroid based inner bounds, and information geometric properties of entropic region.
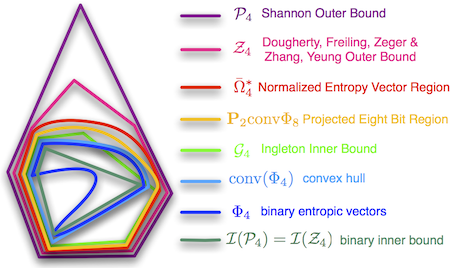
Binary Region of Entropic Vectors
N* is difficult to characterize for arbitrary N ≥ 4, as Mat¨š recently definitively
proved [B12], because there are an infinite number of associated linear
information inequalities. There are few known computationally tractable inner
bounds for N* for N ≥ 4 [B13] [B3], and it is generally unknown how to
determine whether a given candidate vector h ∈ R+2N-1
is entropic or not. A
computational algorithm capable of determining whether or not h ∈N*
is not presently available for N ≥ 4. Our work [A4, A5] points out that
by restricting the discrete random variables to be binary, one can obtain
efficient descriptions of the entropy region, called the set of binary entropic
vectors, ΦN. In particular, we introduce an algorithm which can definitively
determine whether a candidate vector h ∈ R+2N-1
can be generated by a
distribution on N bits. This has enabled us to deliver in [A6, A7, A5] our
primary contribution: an algorithm which, given any polytope outer bound for
convΦN( ), returns a tuned inner bound agreeing on all of its (tight) exposed faces
shared with convΦN(
), returns a tuned inner bound agreeing on all of its (tight) exposed faces
shared with convΦN(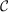 ). Because the inner bounds have this property, their
performance increases with increasingly better performing outer bounds. The inner
bound technique is easily extended to obtaining bounds for convN*(
). Because the inner bounds have this property, their
performance increases with increasingly better performing outer bounds. The inner
bound technique is easily extended to obtaining bounds for convN*(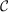 ) and
convN*(
) and
convN*(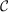 ) as a function of outer bounds for these sets, as they contain
convΦN(
) as a function of outer bounds for these sets, as they contain
convΦN(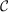 ).
).
Our current work is applying these inner bound techniques to gain insights about the tightness of existing outer bounds for N*, and is dedicated to finding as many extreme points of N* as possible.
Inner Bounds from Representable Matroids & Linear Polymatroids
Matroid theory [B14] is an abstract generalization of independence in the context of linear algebra to the more general setting of set systems. Though there are many classes of matroids, we are especially interested in one of them, representable matroids, because they can be related to linear codes to solve network coding problems as discussed in [A8, A9, A1]. A major direction for this research utilizes (representable) matroids, linear polymatroids, and linear codes to characterize the inner bounds on N*. We use enumeration tools to obtain the list of (binary and ternary) representable matroids and linear codes. The conic hull of rank functions of these matroids (or codes) give us an inner bound that can be used to determine the linear codes achievable rate regions for networks, as discussed in our network coding project.
There exist some enumeration tools for matroid enumeration using single-element-extension [B15]. One can get representable ones from the entire list of matroids by checking if the matroids have forbidden minors for the associated representability. However, the enumeration of matroids only goes to less than or equal to 9 elements, due to the double exponentially increase as the ground set size increases, as Fig. 2 shows. Adapting the enumeration tool with forbidden minor characterization of representable matroids enables us to directly enumerate representable ones. We can easily push the enumeration of binary, ternary representable matroids to ground set size 12, as shown in Fig. 2. As stated above, one of the applications of the representable matroid inner bound is to bound the network rate region. The linear space that the network variables can span determines the rank of representable matroids we need to use. If we only enumerate matroids with ranks up to a particular number, we can go further on the enumeration of both general matroids and representable ones. Our recent work [A1] showed that one can further integrate the network constraints in the enumeration to reduce the enumeration load, as shown in Fig. 2.
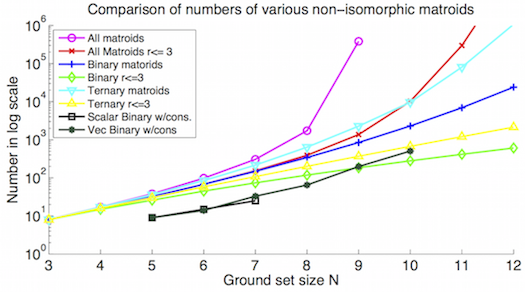
Fig. 2: Number of different types of matroids. The enumeration load can be reduced by integrating the forbidden minor characterization of representable matroids, rank constraint and/or network constraints with matroid enumeration.
Our another recent work [A2] on this project also proved some important properties on the matroid, especially representable matroid bounds. It was shown that the extreme rays of representable matroid inner bound form a subset of extreme rays of matroid bound, which themselves form a subset of extreme rays of the Shannon outer bound. This implies that once we have extreme rays of Shannon, we can do some verification on them to determine the matroid and representable matroid inner bounds. The relations between different bounds related with matroids on 5,6,7 elements is shown in Fig. 3.
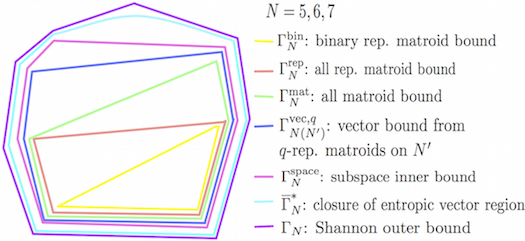
Fig. 3: Different bounds on the region of entropic vectors related with matroids. The extreme rays of them have strict containment relationships.
Information Geometric characterization of the Entropy Region N*
The field of information geometry [B16] is a mathematical science which treats sets
of probability distributions as a differential geometric manifold with an endowed
dually flat geometric structure. The idea is to think of a given probability
distribution as a point in a space (through a smooth parameterization), and the
collection of such points as a manifold. Of significant interest are natural
parameterizations of families of probabilities distributions, especially exponential
families, and how the endowed geometric structure implies fundamental limits
for estimation within these families due to the Cramer-Rao lower bound.
Information geometry endows a manifold of probability distributions p(x;ξ), parameterized by a vector of real numbers ξ = [ξi], with a Riemannian metric, or inner product between tangent vectors, given by the Fisher information:
![∂logp(x;ξ)∂logp(x;ξ)
gi,j(ξ) ≜ Eξ[ ∂ξi ∂ξj ]](entropic0x.png) | (1) |
This allows us to calculate an inner product between two tangent vectors c = ∑ ici∂ξi and d = ∑ idi∂ξi at a particular point ξ in the manifold of probability distributions, as
 | (2) |
Selecting this Riemannian metric (indeed, we could have selected others), and some additional structure, allows the differential geometric structure to be related to familiar properties of exponential families and mixture families of probability distributions. The additional structure, called an affine connection(Fig. 4), is given to the manifold to allow us establish a correspondence, called parallel translation, between tangent vectors living the tangent space at two different points along a curve in the manifold by solving a system of ordinary differential equations involving given functions on the manifold called connection coefficients. Just as with a Riemannian metric, we have an infinite number possible of choices for the affine connection (embodied by selecting connection coefficients with respect to a particular parametrization), but if we choose particular ones, called the α-connections, certain differential geometric notions like flatness and autoparallel submanifolds can be related to familiar notions of probability distribution families/subfamilies like exponential families and mixture families.
Fig. 4: Affine Connection.
The natural divergence functions arising in information geometry, which include the Kullback Leibler divergence, can easily be related to the Shannon entropy by measuring the divergence with the uniform distribution. Additionally, one could think of entropic vectors as characterizing simultaneous properties (entropies) of marginal distributions on subsets of variables, and this simultaneous marginal distribution relationship has a well studied structure in information geometry. Thus characterizing the region of entropic vector could be though of as a problem in information geometry [A3]. Along this line of work, it was first shown that Shannon facets possess certain information geometric properties, for example, Shannon facets was associated with affine subsets of family of probability distribution when it is regarded in an appropriate parameterization, also the submodularity of the entropy function can be viewed as a consequence of pythagorean style information projection relationships. Furthermore, we have shown that a special type of 4 atom support (0000)(0110)(1010)(1111) has a very natural information geometric explanation(Fig. 5).
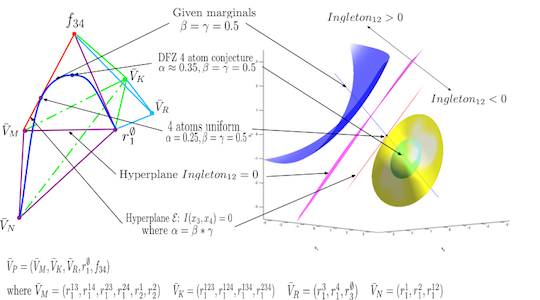
Fig. 5: Characterization of 4 atoms supports with Information Geometry.
Funding for this Topic:
 This work supported by the National Science Foundation under the CAREER
award CCF-1053702 and CCF-1016588.
This work supported by the National Science Foundation under the CAREER
award CCF-1053702 and CCF-1016588.
Relevant Publications & Presentations
[A1] J. Apte, C. Li, and J. Walsh, “Algorithms for computing network coding rate regions via single element extensions of matroids,” in 2014 IEEE International Symposium on Information Theory (ISIT), June 2014.
[A2] C. Li, J. Walsh, and S. Weber, “Matroid bounds on the region of entropic vectors,” in 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton), 2013, Oct 2013, pp. 796–803.
[A3] Yunshu Liu, John MacLaren Walsh, “Bounding the entropic region via information geometry,” in IEEE Information Theory Workshop, Sep. 2013. [Online]. Available: http://www.ece.drexel.edu/walsh/ITW2013_Liu.pdf
[A4] John MacLaren Walsh and Steven Weber, “A Recursive Construction of the Set of Binary Entropy Vectors,” in Forty-Seventh Annual Allerton Conference on Communication, Control, and Computing, Sep. 2009, pp. 545–552. [Online]. Available: http://www.ece.drexel.edu/walsh/binEntSetConf-v5-JW.pdf
[A5] J. M. Walsh and S. Weber, “A Recursive Construction of the Set of Binary Entropy Vectors and Related Inner Bounds for the Entropy Region,” IEEE Trans. Inform. Theory, vol. 57, no. 10, pp. 6356–6363, Oct. 2011. [Online]. Available: http://dx.doi.org/10.1109/TIT.2011.2165817
[A6] John MacLaren Walsh and Steven Weber, “Tunable Inner Bounds for the Region of Entropy Vectors,” Feb. 2010, 2010 Information Theory and Applications Workshop, University of California San Diego. [Online]. Available: http://www.ece.drexel.edu/walsh/walshITA10.pdf
[A7] ——, “Relationships Among Bounds for the Region of Entropic Vectors in Four Variables,” in 2010 Allerton Conference on Communication, Control, and Computing, Sep. 2010. [Online]. Available: http://www.ece.drexel.edu/walsh/allerton10.pdf
[A8] C. Li, J. Apte, J. M. Walsh, and S. Weber, “A new computational approach for determining rate regions and optimal codes for coded networks,” in IEEE International Symposium on Network Coding (NetCod), Jun 2013, pp. 1 –6.
[A9] C. Li, J. M. Walsh, and S. Weber, “Computational approaches for determining rate regions and codes using entropic vector bounds,” in 50th Annual Allerton Conference on Communication, Control and Computing, Oct 2012, pp. 1 –9.
[A10] John MacLaren Walsh and Steven Weber, “An Inner Bound Technique on the Normalized Set of Entropy Vectors,” Sep. 2009, DARPA ITMANET Meeting, MIT. [Online]. Available: http://www.ece.drexel.edu/walsh/weberITMANET0909.pdf
[A11] ——, “Properties of the Binary Entropy Vector Region,” Mar. 2009, DARPA ITMANET Meeting, Stanford University. [Online]. Available: http://www.ece.drexel.edu/walsh/weberITMANET0309.pdf
[A12] John MacLaren Walsh, Steven Weber, Drakontas LLC, “Optimal Coded Information Network Design and Management via Improved Characterizations of the Binary Entropy Function,” Feb. 2009, Air Force Office of Scientific Research Complex Network Program Review. [Online]. Available: http://www.ece.drexel.edu/walsh/walshAFOSR09.pdf
External References
[B1] Raymond W. Yeung, Information Theory and Network Coding. Springer, 2008.
[B2] B. Hassibi and S. Shadbakht, “Normalized Entropy Vectors, Network Information Theory and Convex Optimization,” in IEEE Information Theory Workshop on Information Theory for Wireless Networks, Jul. 2007, pp. 1 – 5.
[B3] ——, “On a Construction of Entropic Vectors Using Lattice-Generated Distributions,” in IEEE International Symposium on Information Theory (ISIT), Jun. 2007, pp. 501 – 505.
[B4] Zhen Zhang and Raymond W. Yeung, “A Non-Shannon-Type Conditional Inequality of Information Quantities,” IEEE Transactions on Information Theory, vol. 43, no. 6, Nov. 1997.
[B5] ——, “On Characterization of Entropy Function via Information Inequalities,” IEEE Transactions on Information Theory, vol. 44, no. 4, Jul. 1998.
[B6] R. Dougherty, C. Freiling, and K. Zeger, “Networks, Matroids, and Non-Shannon Information Inequalities,” IEEE Transactions on Information Theory, vol. 53, no. 6, pp. 1949–1969, Jun. 2007.
[B7] F. Mat˙š and M. Studený, “Conditional Independences among Four Random Variables I,” Combinatorics, Probability and Computing, no. 4, pp. 269–278, 1995.
[B8] F. Mat˙š, “Conditional Independences among Four Random Variables II,” Combinatorics, Probability and Computing, no. 4, pp. 407–417, 1995.
[B9] ——, “Conditional independences among four random variables III: final conclusion.” Combinatorics, Probability and Computing, no. 8, pp. 269–276, 1999.
[B10] Xijin Yan, Raymond W. Yeung, and Zhen Zhang, “The Capacity Region for Multi-source Multi-sink Network Coding,” in IEEE International Symposium on Information Theory (ISIT), Jun. 2007, pp. 116 – 120.
[B11] T. Chan and A. Grant, “Entropy Vectors and Network Codes,” in IEEE International Symposium on Information Theory, Jun. 2007.
[B12] František Mat˙š, “Infinitely Many Information Inequalities,” in IEEE International Symposium on Information Theory (ISIT), Jun. 2007, pp. 41–44.
[B13] T. Chan and R. Yeung, “On a relation between information inequalities and group theory,” IEEE Transactions on Information Theory, vol. 48, no. 7, pp. 1992 – 1995, Jul. 2002.
[B14] J. G. Oxley, Matroid Theory. Oxford University, 2011.
[B15] D. Mayhew and G. F. Royle, “Matroids with nine elements,” Journal of Combinatorial Theory, Series B, vol. 98, no. 2, pp. 415 – 431, 2008.
[B16] S. Amari and H. Nagaoka, Methods of Information Geometry. American Mathematical Society Translations of Mathematical Monographs, 2004, vol. 191.
