• Home
• Research
• Software
• Facilities
• People
• Publications
• Contact us

Collaborative estimation refers to a scenario in which a collection of networked nodes making local observations exchange information with one another in hopes of better estimating a common underlying sequence of parameters. Of chief interest in this family of problems is the selection of the structure and contents of the messages to be passed between the nodes as well as the local processing necessary to form the local estimates. When designing a collaborative estimation algorithm, two types of constraints must be considered. First of all, collecting multiple nodes observations can lead to a complex statistical model in which to do estimation, in which case the constraints of the computational complexity of the estimation algorithm are important considerations. Second of all, information exchange between the nodes must be done over finite rate communications links which can require significant power consumption, so communication rate and amount considerations are important. Classic theoretical disciplines can be applied to develop collaborative estimation algorithms according to how stringent these two constraints are, as depicted in Table 1 below. If neither of the constraints are stringent the nodes can merely share all of their observations directly with one another and calculate joint Bayesian estimates.

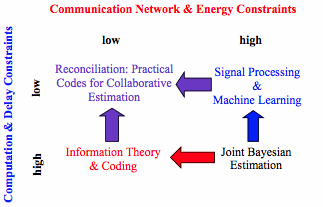
1. Complexity - low / Communication - high
   When complexity constraints are stringent, and communications constraints are less important, message passing algorithms from machine learning can provide principled approaches for deriving collaborative estimation algorithms. In particular, message passing approximate Bayesian inference techniques can allow high performance estimates to be obtained with a lower complexity than working with the true model. Our work in this area designed a collaborative estimation algorithm based on Expectation Propagation (EP), a family of approximate Bayesian inference algorithms, which has low complexity and high communication requirements. EP exploits the factors of joint probability density function to approximate it as product of exponential family densities.

   Our work has shown the natural candidacy of the expectation propagation for collaborative estimation in sensor networks and demonstrated the viability of expectation propagation in common sensor network tasks. Finally, we have bounded the performance in the large system limit by applying performance and convergence techniques to the statistical models of these applications. For more details, see [8, 10, 11, 12, 13, 14, 15].

2. Complexity - high / Communication - low
   A coding and information theoretic approach to designing collaborative estimation algorithms studies estimation performance attainable under strict and explicit communications constraints but with no limitations placed on complexity. Hence much can be gained from modeling collaborative estimation as a multiterminal rate distortion theory problem when the centralized estimation problem of interest is well within the computational limitations. Of chief interest here is the effect of the limitations of the communications network on the performance of the estimation problem.

   Our work in this area has proceeded by first determining the general structure that such codes for collaborative estimation must have, arguing via a series of examples that they should consist of multiple multicast descriptions in order to best interface with the capabilities of the network. The relationship between the collaborative estimation problem and an associated lossy source coding problem is discussed. The associated network lossy source coding problem is shown to have a hybrid nature between two classic problems in multi-terminal information theory: the CEO problem and the multiple descriptions problem. The rate distortion region for this hybrid lossy source coding problem yields the relationship between the set of rates of the multicast messages and Bayesian estimation errors (distortions) that can be achieved at the nodes. We derive inner and outer bounds for the rate distortion region by extending techniques from these two classic problems [6, 7, 9, 2]. The inner and outer bounds are shown to match in some special cases, yielding the exact rate distortion region and hence a characterization of the most efficient collaborative estimation schemes in these cases.

3. Complexity - low / Communication - low
   Ideally a collaborative estimation algorithm would optimize estimate performance to be the highest possible while obeying explicit communication and complexity constraints. The solutions here share aspects with the solutions for the previous two problems, and can be considered as practical source codes: efficient codes must be designed with low complexity decoders. Our work in this domain looks at ways to adapt powerful channel coding techniques such as LDPC and Turbo codes, which are both efficient and have low complexity belief propagation decoders, to build collaborative estimation algorithms.

   Our initial work on this problem has developed practical codes for variants of the problem of “source coding when side information may be absent” depicted in Fig. 1. Extensions of this model are useful for designing collaborative estimation algorithms in networks where different nodes make corrupted observations of the underlying source of varying quality. The fundamental rate distortion limitations for this problem were determined in a seminal paper by Heegard and Berger, and our aim was to mimic their theoretical construction with a practical code.

   

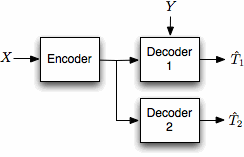
   Fig. 1: Network model for the side information may be absent problem.

   We have applied successively refinable trellis coded quantization (SR-TCQ) to generate common message to both decoders and an individual message to the decoder with side information [3, 4, 2]. The common message is then compressed using universal source coding techniques and the individual message is compressed by sending a LDPC code syndrome, which allows us to exploit the correlation between the observations at the encoder and decoder. This code construction has low complexity and low communication requirements.

   Our current work is extending these techniques further to construct codes for more complex network estimation problems.

Research Collaborators on this Topic: Dr. Phillip Regalia, Catholic University of America.

Funding for this Topic:

This work has been supported by the National Science Foundation under the awards CCF-0728496 and CCF-1053702.

Relevant Publications & Presentations