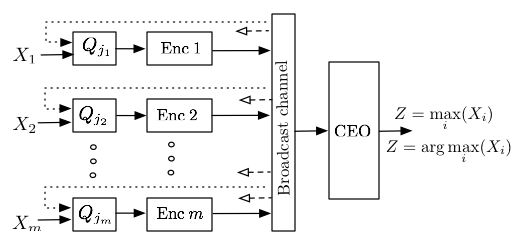
Distributed Function Computation: Rate regions, Quantization, and Interactive Communication
Distributed source coding (DSC) is an important problem in information theory which concerns the compression of multiple correlated information sources that do not communicate with each other. In DSC, the goal is to recover the source symbols only. However, in some applications if the receiver is interested in only computing a function (or some functions) of sources, thereby enabling further compression. This generic distributed function computation problem arises in several fields. We consider the following five examples here.
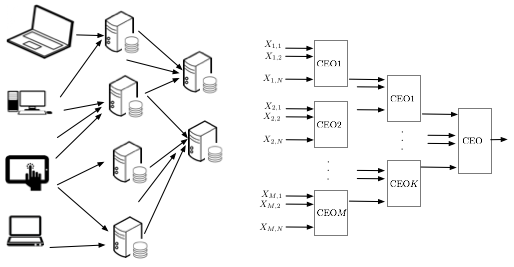
Example 1 (Big data processing). In big data problems, the major issue is to design computational methodologies suited to calculating statistics that are meaningful for learning from the data, in a manner which scales efficiently as the data being processed becomes immense. Of interest is the fundamental problems in massive datasets where some statistical primitives need to be computed for some machine learning or data analysis tasks for datasets stored in large distributed storage systems. In a massively parallel computing paradigm, one of the most significant bottlenecks is the communication between the processors. Hence, when computing important statistics from massive datasets minimizing data transfer can be a key step in enhancing performance and scalability. This motivates our research which aims to determine the communication architecture and codes achieving the fundamental minimum amount of information that must be exchanged to calculate each statistic of interest.
Example 2 (OFDMA resource allocation).
In a multiuser OFDMA system, the base station (BS) needs to assign mobile stations (MSs) to subblocks of channels. This is referred to as the resource allocation problem [A1]. If the BS wishes to maximize the sum-rate across users, the uplink feedback from the MS needs to enable the basestation to determine which MS has the best channel. For each of the resource subblocks, when conventional channel codes are used in the downlink data transmission, the BS needs to know both who has the best channel and the best channel quality to utilize the adaptive and modulation coding (AMC) scheme. With a proper assumption that the channel quality of all MSs on the same subblock are i.i.d. random variables, this is equivalent to finding max and arg max across all users on each subblocks. When a rateless code is used in the downlink data transmission, the BS only needs to know who has the best channel (finding only arg max, Figure 2). Once the BS has decided which user to schedule on a particular collection of subbands, it must signal this resource decision on the downlink as overhead control information in addition to the data to be transmitted to the user itself. Our interest is to understand how to efficiently encode the control information so that the BS can decide the arg max.
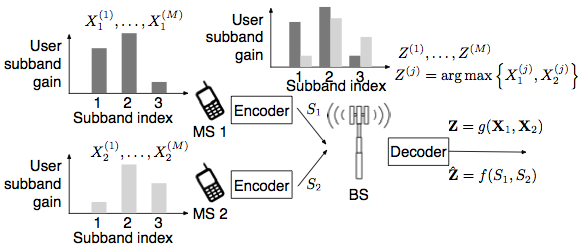
Example 3 (Sealed-bid first-price auctions). When a seller has a commodity that it wishes to sell, it sets the price with respect to the market. If the seller wants to ensure that it does not price itself out of the market, it would want to compute the max of the individual valuations of a representative sample of the market.We think of the CEO selling a good through an auction to a set of independent buyers. In a sealed-bid first-price auction, the buyers submit bids in “sealed” envelopes and the highest bidder is the winner, paying their bid amount. The auctioneer has no need for recovering the bids of the other users.
Example 4 (sensor network/intrusion detection). A collection of sensor
nodes are monitoring an area large enough that individual sensor readings
are independent. As a very simple model, we can take the local sensor outputs
to be binary: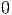 
if no intruder is present, 
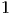if an intruder is present.
Computing the 
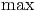sensor reading determines if an intruder is present but
not where; computing the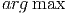 
determines where an intruder is (if in
fact there is one), and; computing both determines if and where an intruder
is.
Example 5 (information retrieval). Increasingly information is being stored in distributed data structures because the data is inherently distributed, in an attempt to improve system performance (e.g., availability, look-up latency, etc.), or because the data set is too large to be effectively collocated. When analyzing this data, often times what needs to be reported is not the full set of data but some reduction of the data. Reducing the rate to compute the function of the data can be led to lower query times and less utilization of the network connecting the distributed storage pools.
1 Lossless function computation
By lossless computation, we mean asymptotically lossless computation of a function: the error probability goes to zero as the block length goes to infinity. The two-terminal function computation with side information problem has been considered in [B1] where two terminals (transmitter and receiver) each contain a source and the receiver wants to decode a function of the two sources. Orlitsky et al. considered the problem of minimizing the encoder’s alphabet size with vanishing probability of error, and showed that the fundamental limit on rate is the graph entropy of the characteristic graph. The distributed function computation problem has been considered in [B2] under the CEO setup [B3], where the CEO wants to compute a function of the sources from two or more users. Doshi et al. gave the rate region to the problem under a constraint that they term a ”zig-zag” condition. They showed that any achievable rate point can be realized by graph coloring at each user and Slepian-Wolf (SW) [B4] encoding the colors.
Although one may think that the best scheme for the CEO computing an objective function with varnishing probability of error is to let each user entropy encode its own source, we have shown that for certain objective functions, information rate savings can be obtained by recognizing that controller only needs to determine the result of the function (Example 6).
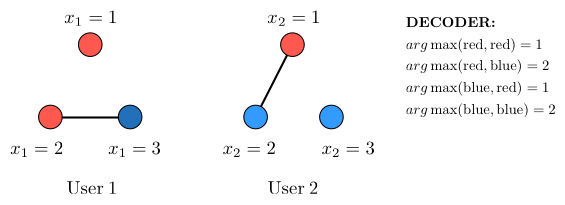
Example 6. Let the 2 users each observe X1 and X2 respectively. Let X1 and X2 be two independent random variables that uniformly distributed over {1, 2, 3}. Let the objective function that the CEO needs to compute be the arg max,
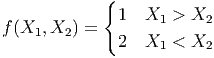 | (1) |
Note that we didn’t clarify the function output when the two users both achieve maximum. We will accept both of the two function outputs when X1 equals to X2 because in the relative resource allocation model, no capacity loss will be induced. Then if the users each entropy encode its source, it will take
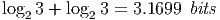 | (2) |
Now if we first assign colors to different outcomes of the source random variables, and entropy encode the colors, it will take
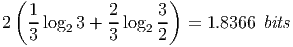 | (3) |
After a simple analysis, we can see that the color messages are sufficient for the CEO to compute the arg max.
Building upon this line of research, we are interested in providing an achievable coding scheme to losslessly compute some statistics of the data. In the recent work [A2][A3], we gave practical schemes that achieve the fundamental limits of the sum rate for losslessly computing extremization functions of independent sources. We also showed that the rate saved by lossless function computation is not substantial. These results motivate us to consider the lossy and interactive variants of the function computation problems.
2 Lossy compression
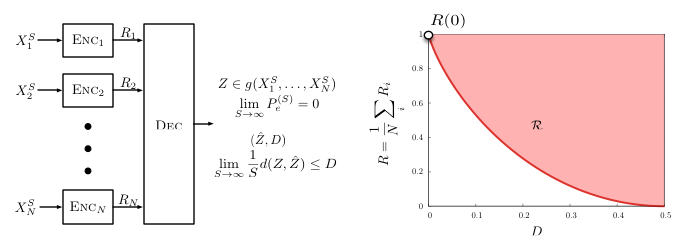
In some cases, the rate can be reduced only by incurring a small penalty. Rate-distortion theory is such an example where the rate required to communicate/reconstruction a signal is can be substantially reduced if small errors in the reconstruction can be tolerated. For point-to-point rate distortion problems, Arimoto and Blahut proposed numerical calculation algorithms based on alternating optimization to find the channel capacity and rate distortion function. We have developed a generalization of the Blahut-Arimoto algorithm to a multi terminal scenario to help us compute the rate distortion region for the distributed function computation with independent sources problem [A4][A2].
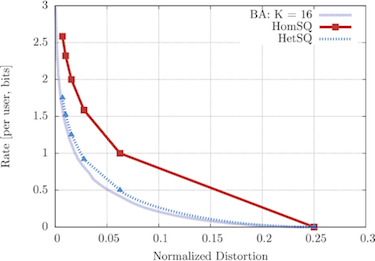
We observed from the resulting bound, a case of which is plotted in Figure 5, that substantial rate savings can be achieved if the controller tolerates even a small amount of distortion in computing, for instance, the arg max function. We have also designed practical encoding schemes for these extremization (max, argmax) functions. In particular, we developed simple scalar quantizers for remote extremization whose rate distortion performance closely matches the optimal rate distortion curve[A5][A2]. Both homogenous designs, which utilize the same scalar quantizer for all users, and heterogeneous designs, which allow different users to use different quantizers, were investigated.
3 Interactive communication
Interactive communication is a scheme that allows message passing over multiple rounds, where at each round, the communicating parties are allowed to send messages based on what they have received in previous rounds as well as their local source observation [B5].
In [A3][A2], [A6], we consider interaction in the distributed function computation model. If no distortion can be tolerated, we demonstrated, by proposing an achievable interactive coding scheme optimized by dynamic programming, that substantial rate savings can still be achieved if the controller and the users are allowed to interactively communicate. In [A6] the interactive CEO problem is investigated with an assumption that, at each round all of the participating users must utilize a common (homogeneous) scalar quantizer, and must transmit their messages at each round in parallel. We consider a simple interactive scheme built from several rounds of scalar quantization followed by Huffman coding.
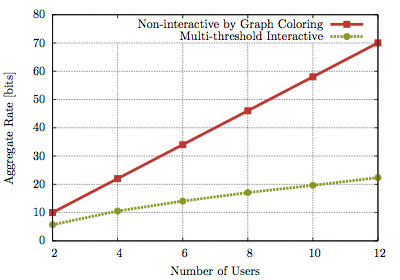
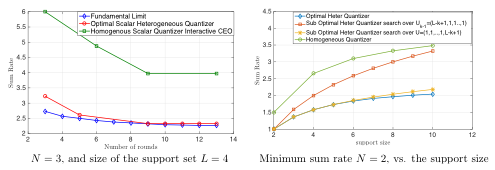
In another type of network so-called collocated network, the users take turns sending messages to the CEO, with each user perfectly overhearing the message from every other user. Ma et al, in [B6] studied this problem in a distributed source coding framework, and proposed an iterative algorithm via a convex geometric approach to compute the minimum sum rate of for any finite and infinite number of rounds. Building upon this prior work, we study the design of interactive scalar quantizers for distributed lossless extremization function computation in the collocated network as demonstrated in Figure 7. After computing the fundamental limit from [B6] for the case of the extrema functions and some small numbers of users and support sizes, we study the the fundamental tradeoff between the rate-cost and the delay in several interactive quantization schemes. We show that using optimal heterogeneous quantizers exploiting overheard messages result in substantial rate savings relative to the parallel homogenous quantizers in [A6]. Finally, we design and analyze low complexity suboptimal schemes with performance close to the optimal sum rate.
It’s shown that a dynamic strategy which involves scalar quantization and Huffman codes using the families of suboptimal quantizers is able to approach the fundamental limit. We also show that the requirement of homogenous quantizers and active users transmitting at each round in parallel in 8 is a distant upper bound to the rate obtainable with the collocated network. Substantial rate savings are enabled by letting the users take turns speaking one at a time and overhear one other.
Research Collaborators on this Topic: Dr. S. Weber (Drexel University), Dr. L. Cimini, Dr. J. Garcia-Frias (University of Delaware).
Funding for this Topic:
This work has been supported in part by the AFOSR award AF9550-12-1-0086.
Relevant Publications & Presentations
[A1] G. Ku and J. M. Walsh, “Resource allocation and link adaptation in lte & lte advanced : A tutorial,” IEEE Communications Surveys and Tutorials, vol. PP, no. 99, p. 1, December 2014.
[A2] J. Ren, B. Boyle, G. Ku, S. Weber, and J. M. Walsh, “Overhead performance tradeoffs - a resource allocation perspective,” submitted to IEEE Trans. Inf. Theory. [Online]. Available: {http://arxiv.org/pdf/1408.3661v1.pdf}
[A3] J. Ren and J. M. Walsh, “Interactive communication for resource allocation,” in Conf. Information Sciences and Systems (CISS), March 2014.
[A4] G. Ku, J. Ren, and J. M. Walsh, “Computing the rate distortion region for the ceo problem with independent sources,” IEEE Transaction on Signal Processing, vol. 63, no. 3, pp. 567–575, February 2015.
[A5] B. D. Boyle, J. M. Walsh, and S. Weber, “Distributed scalar quantizers for subband allocation,” in Conf. Information Sciences and Systems (CISS), March 2014.
[A6] B. Boyle, J. Ren, J. M. Walsh, and S. Weber, “Interactive scalar quantization for distributed extremization,” submitted to IEEE Transactions on Signal Processing. [Online]. Available: {http://arxiv.org/pdf/...}
External References
[B1] A. Orlitsky and J. R. Roche, “Coding for computing,” IEEE Trans. Inform. Theory, vol. 47, no. 3, pp. 903–917, March 2001.
[B2] V. Doshi, D. Shah, M. Medard, and S. Jaggi, “Functional compression through graph coloring,” IEEE Trans. Inform. Theory, vol. 56, no. 8, pp. 3901–3917, August 2010.
[B3] T. Berger, Z. Zhang, and H. Viswanathan, “The ceo problem [multiterminal source coding],” IEEE Trans. Inform. Theory, vol. 42, no. 3, pp. 887–902, May 1996.
[B4] D. Slepian and J. Wolf, “Noiseless coding of correlated information sources,” IEEE Trans. Inform. Theory, vol. 19, no. 4, pp. 471–480, Jul. 1973.
[B5] A. H. Kaspi, “Two-way source coding with a fidelity criterion,” IEEE Trans. Inform. Theory, vol. 31, no. 6, p. 735, November 1985.
[B6] N. Ma, P. Ishwar, and P. Gupta, “Interactive source coding for function computation in collocated networks,” Information Theory, IEEE Transactions on, vol. 58, no. 7, pp. 4289–4305, 2012.