Performance and Convergence of Expectation and Belief Propagation

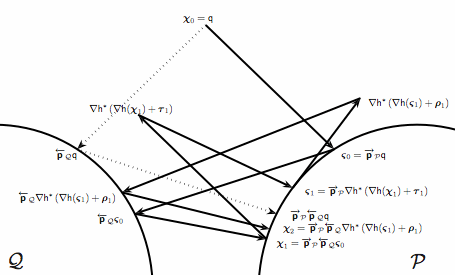
Expectation and (loopy) belief propagation are methods for approximate iterative statistical inference that have found extensive cutting edge applications in machine learning, pattern recognition, computer vision, multiuser communications, and even missile defense. These methods are heuristic in nature, only performing approximate statistical inference, and, despite their ever growing widespread application, the mechanisms underlying their empirically observed frequently good performance and convergence behavior remain not well understood. Our research has shown that these methods may be interpreted as a hybrid between two iterative projections methods from the convex programming community: alternating Bregman projections, and Dykstra’s algorithm with cyclic Bregman projections. The projections and sets themselves are information geometric, asymmetric, and are not convex in the same coordinate system, but when they are replaced with normal Euclidean orthogonal projections and convex sets, a provably convergent algorithm is obtained (Figure 1). Furthermore, this Euclidean version of belief propagation frequently converges to the vicinity of the desired two step projection that optimal inference would perform (dotted lines above). Theorems about the performance and convergence behavior or normal belief propagation are being developed through this connection. We are also seeking insights about the performance and convergence behavior of these algorithms using other tools, including extensions of EXIT chart and density evolution tools developed for the iterative decoding (error control coding) community as well.

PIC


Figure 1: Belief propagation may be interpreted as an iterative information geometric projections algorithm between two sets with Dykstra’s algorithm-like preprocessing between projections. The solid lines in the graph above shows an example of this iterative projections algorithm, dubbed Euclidean belief propagation, when the projections are replaced with normal Euclidean orthogonal projections. The dotted lines represent a difficult (optimal) projection which belief propagation is iteratively trying to approximate using many easier to perform projections.

Research Collaborators on this Topic: Dr. Phillip Regalia, Catholic University of America. A couple of discussions with Dr. Pierre Duhamel and Dr. Florence Alberge, Supélec, Paris, France.

Funding for this Topic:

PIC Partially supported by the National Science Foundation under the awards CCF-0728496 & CCF-1053702.

Relevant Publications & Presentations

[1]   J. M. Walsh and P. A. Regalia, “Belief Propagation, Dykstra’s Algorithm, and Iterated Information Projections,” IEEE Trans. Inform. Theory, vol. 56, no. 8, pp. 4114–4128, Aug. 2010. [Online]. Available: http://dx.doi.org/10.1109/TIT.2010.2050833

[2]   Phil Regalia and John MacLaren Walsh, “Information Projection Algorithms and Belief Propagation,” Jun. 2008, P. Dewilde Workshop, Wassenaar. [Online]. Available: http://www.ece.drexel.edu/walsh/regalia-wassenaar-talk.pdf

[3]   John MacLaren Walsh, “Belief Propagation, Information Projections, and Dykstra’s Algorithm,” Apr. 2008, MIT Workshop on Geometric Approaches in Communications and Signal Processing. [Online]. Available: http://www.ece.drexel.edu/walsh/walshMITW08.pdf

[4]   P. A. Regalia and J. M. Walsh, “Optimality and Duality Aspects of the Turbo Decoder,” Proc. IEEE, vol. 95, no. 6, pp. 1362–1377, Jun. 2007. [Online]. Available: http://dx.doi.org/10.1109/JPROC.2007.896495

[5]   J. M. Walsh and P. A. Regalia, “On the relationship between belief propagation decoding and joint maximum likelihood detection,” IEEE Trans. Commun., vol. 58, no. 10, pp. 2753–2758, Oct. 2010. [Online]. Available: http://dx.doi.org/10.1109/TCOMM.2010.082010.080138

[6]   J. M. Walsh, P. A. Regalia, and C. R. Johnson, Jr., “Turbo Decoding as Iterative Constrained Maximum-Likelihood Sequence Detection,” IEEE Trans. Inform. Theory, vol. 52, no. 12, pp. 5426–5437, Dec. 2006. [Online]. Available: http://dx.doi.org/10.1109/TIT.2006.885535

[7]   J. M. Walsh, “A completed information projection interpretation of expectation propagation,” in Neural Information Processing Systems Workshop on Approximate Bayesian Inference in Continuous/Hybrid Systems, 2007. [Online]. Available: http://www.ece.drexel.edu/walsh/epInfProjNips07.pdf

[8]   ——, “EXIT and Density Evolution Analysis for Homogeneous Expectation Propagation,” in IEEE International Symposium on Information Theory, Nice, France, Jul. 2007, pp. 876–880. [Online]. Available: http://www.ece.drexel.edu/walsh/isit07.pdf

[9]   ——, “Density evolution for expectation propagation,” in International Conference on Acoustics, Speech, and Signal Processing (ICASSP), vol. 2, Honolulu, Hawaii, Apr. 2007, pp. II–545 – II–548. [Online]. Available: http://www.ece.drexel.edu/walsh/icassp07.pdf

[10]   ——, “Dual optimality frameworks for expectation propagation,” in Proc. Seventh IEEE Int. Conf. on Sig. Proc. Adv. in Wireless Comm. (SPAWC), Jul. 2006. [Online]. Available: http://www.ece.drexel.edu/walsh/spawc06.pdf