Monte Carlo Simulations in the Isothermal-Isobaric (NPT) and Grand Canonical (
Isothermal-Isobaric (NPT)
In this section, we consider how to conduct Monte Carlo simulation in
ensembles other than the canonical ensemble. In deriving the
partition function for the canonical ensemble
(Eq. 42), we imagined our sytem of constant ![]() ,
,
![]() , and
, and ![]() in thermal contact with a large reservoir. This thermal
contact allowed the system and reservoir to exchange energy such that
the system remained at constant
in thermal contact with a large reservoir. This thermal
contact allowed the system and reservoir to exchange energy such that
the system remained at constant ![]() , and what resulted was the
Boltzmann factor. In Section 5.4.1, F&S explain the case when we
have the reservoir and the system both thermally and mechanically coupled. The mechanical coupling allows the volume of
the system to change such that the pressure in the system is the same
as the reservoir, which is again considered as an inifinite ideal gas.
In addition to thermostatting our system, the reservoir acts as a barostat.
, and what resulted was the
Boltzmann factor. In Section 5.4.1, F&S explain the case when we
have the reservoir and the system both thermally and mechanically coupled. The mechanical coupling allows the volume of
the system to change such that the pressure in the system is the same
as the reservoir, which is again considered as an inifinite ideal gas.
In addition to thermostatting our system, the reservoir acts as a barostat.
First, for convenience, we express the set of coordinates, ![]() , scaled by the box length,
, scaled by the box length, ![]() , as
, as ![]() . The partition
function in the NPT ensemble is then
. The partition
function in the NPT ensemble is then
| (164) |
| (165) |
Now, compared to the canonical ensemble, in the NPT ensemble, volume
is an additional degree of freedom. We need the probability
distribution to include volume:
| (166) | |||
| (167) |
| (168) |
We can also consider trial move that changes the logarithm of the box
size from ![]() to
to
![]() . In this
case, the integral of
. In this
case, the integral of ![]() over
over ![]() is re-expressed as an integral
of
is re-expressed as an integral
of ![]() over
over ![]() , and the acceptance rule is the same as the
one above except for a factor of
, and the acceptance rule is the same as the
one above except for a factor of ![]() multiplying
multiplying ![]() ,
instead of
,
instead of ![]() .
.
The C-code mclj_npt.c
implements
an NPT MC simulation of the Lennard-Jones liquid using both particle
displacements and log-![]() displacements. For each cycle, there is a
displacements. For each cycle, there is a
![]() probability that a trial move is a volume displacement. The
trial move generates a random displacement, computes a new box length,
rescales all particle positions, scales the cutoff radius, and
recomputes the tail corrections and shift, if applicable. If the
Metropolis criterion is not met after a random number is selected,
then all of these operations are undone. Otherwise, the new box size
with the newly scaled particle positions is kept. The particle
displacement algorithm is the same as in mclj.c.
probability that a trial move is a volume displacement. The
trial move generates a random displacement, computes a new box length,
rescales all particle positions, scales the cutoff radius, and
recomputes the tail corrections and shift, if applicable. If the
Metropolis criterion is not met after a random number is selected,
then all of these operations are undone. Otherwise, the new box size
with the newly scaled particle positions is kept. The particle
displacement algorithm is the same as in mclj.c.
As an exercise, you can use the code to regenerate Figure 5.3 in the
text, which is again a slice through the phase diagram of the
Lennard-Jones fluid at ![]() = 2.0. This temperature is above the
critical tempeerature, so we do not anticipate a phase transition at
the pressures investigated. However, we saw that when we considered
= 2.0. This temperature is above the
critical tempeerature, so we do not anticipate a phase transition at
the pressures investigated. However, we saw that when we considered
![]() = 0.9 using the NVT MC simulation, negative pressures were
predicted, indicating that the system would have liked to phase
separate but couldn't due to its fixed density and finite size. That
is, at the density specified, there might not be enough particles to
``nucleate'' the denser of the two phases. NPT simulations in
principle offer a way around that by allowing the system density to
fluctuate.
= 0.9 using the NVT MC simulation, negative pressures were
predicted, indicating that the system would have liked to phase
separate but couldn't due to its fixed density and finite size. That
is, at the density specified, there might not be enough particles to
``nucleate'' the denser of the two phases. NPT simulations in
principle offer a way around that by allowing the system density to
fluctuate.
I ran the code with ![]() = 108 particles for 10
= 108 particles for 10![]() cycles. 1 The log-volume maximum
displacement was set at 0.25, and the maximum particle displacement
varied from 0.3 for
cycles. 1 The log-volume maximum
displacement was set at 0.25, and the maximum particle displacement
varied from 0.3 for ![]() , to 0.5 at the lowest value of
, to 0.5 at the lowest value of ![]() . You can
see from the figure below that the data at
. You can
see from the figure below that the data at ![]() = 2.0 is equally well
reproduced here as it was using conventional NVT MC. However, for
= 2.0 is equally well
reproduced here as it was using conventional NVT MC. However, for ![]() = 0.9, we notice that the densities which arise are clearly indicate a
high-density phase is prevalent. As suggested in F&S, this code
also computes the pressure from the virial, and the measured pressure
and imposed pressures agreed, as you can see from the table.
= 0.9, we notice that the densities which arise are clearly indicate a
high-density phase is prevalent. As suggested in F&S, this code
also computes the pressure from the virial, and the measured pressure
and imposed pressures agreed, as you can see from the table.
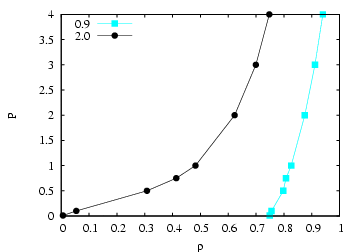 |
|
|
|
|
|
| 0.0100 | 0.0115 |
| 0.100 | 0.101 |
| 0.500 | 0.500 |
| 0.750 | 0.743 |
| 1.000 | 0.992 |
| 2.000 | 2.002 |
| 3.000 | 2.996 |
| 4.000 | 3.977 |
For temperatures near the critical temperature, we would expect the
fluctuations in density to be maximum. As an exercise, you can modify
mclj_npt.c to compute the average fluctuations in ![]() .
.
Grand Canonical (![]() VT)
VT)
So we see that volume exchanges with an ideal gas reservoir can
be used to fix the pressure of a test system. Similarly, particle exchanges with an ideal gas reservoir can be used to fix the
chemical potential of a test system. Chemical potential is defined as
the change in free energy with particle number:
| (169) |
For an ideal gas, we know that the NVT partition function is given
by
| (170) |
| (171) |
| (172) |
Sec. 5.6 in F&S is devoted to explaining the implementation of a
grand canonical MC simulation. The basic idea is that we allow our
system to interact with an ideal gas system at a fixed ![]() (which is
related to a fixed
(which is
related to a fixed ![]() , as discussed in Appendix G) by exchanging
particles. The appropriate probability density is
, as discussed in Appendix G) by exchanging
particles. The appropriate probability density is
| (173) |
To implement a random walk with this probability distribution, in
addition to the normal particle displacement moves, we also have
insertion and removal of particles with appropriate acceptance ratios:
![$\displaystyle {\rm min}\left[1,\frac{V}{\Lambda^3\left(N+1\right)}\exp\left\{
\...
...-\mathscr{U}\left(N+1\right) + \mathscr{U}\left(N\right)
\right]\right\}\right]$](img532.png) |
(174) | ||
![$\displaystyle {\rm min}\left[1,\frac{\Lambda^3N}{V}\exp\left\{
\beta\left[\mu-\mathscr{U}\left(N-1\right) - \mathscr{U}\left(N\right)
\right]\right\}\right]$](img534.png) |
(175) |
So, we can specify ![]() of the ideal gas bath, specify
of the ideal gas bath, specify ![]() and
and ![]() ,
and conduct a grand canonical MC simulation, and measure pressure,
density, and excess chemical potential in our system of
interest. The code for Case Study 9 in F&S is available at the
book's
website: http://molsim.chem.uva.nl/frenkel_smit/.
As an exercise, and to have an opportunity to see how someone else
writes a simulation code, I recommend that you download this program
and try to compile and run it. You will see three directories: Run,
Source, and Block; Source contains the FORTRAN source code, and Run
contains input files and a run script. Block contains the code for
computing block averages; my version of this code is flyvbjerg.c. The file you download is CaseStudy_9.tar.gz,
which is a gzipped tar archive (sometimes referred to as a
``tarball''). You can unpack it under Cygwin using
,
and conduct a grand canonical MC simulation, and measure pressure,
density, and excess chemical potential in our system of
interest. The code for Case Study 9 in F&S is available at the
book's
website: http://molsim.chem.uva.nl/frenkel_smit/.
As an exercise, and to have an opportunity to see how someone else
writes a simulation code, I recommend that you download this program
and try to compile and run it. You will see three directories: Run,
Source, and Block; Source contains the FORTRAN source code, and Run
contains input files and a run script. Block contains the code for
computing block averages; my version of this code is flyvbjerg.c. The file you download is CaseStudy_9.tar.gz,
which is a gzipped tar archive (sometimes referred to as a
``tarball''). You can unpack it under Cygwin using
cfa@abrams01:/home/cfa> tar zvxf CaseStudy_9.tar.gzThen, to compile, change directory into CaseStudy_9/Source, and use the make command:
cfa@abrams01:/home/cfa> cd CaseStudy_9/Source cfa@abrams01:/home/cfa/CaseStudy_9/Source> make clean cfa@abrams01:/home/cfa/CaseStudy_9/Source> makeThe make clean command removes the object files (those that end with o), which are presumably included because F&S assume you are going to run on a Linux PC. The second make compiles the program. You should repeat this procedure in the Block directory to build the block average program, which is used in the run script. Then, you can change directory to the Run directory and begin simulating.
We can run this code by specifying the pressure of the ideal gas bath, the temperature, and the initial density and number of particles, which sets the volume. The run script, run, has a loop structure in it (a ``foreach'' loop) which in principle allows the user to run multiple bath pressures. The output is appended to a file called out, which you can process (using grep, for example) to extract results. Simply add more ideal gas pressures in the parentheses:
foreach pid (0.016 0.032 0.064 )
There is, however, a little bug in the run script. The copy command (the first command in the script) should be inside the loop, because the last command in the body of the loop removes all files whose name begin with ``fort.'' Original:
cp lj.model fort.25 foreach pid (0.016 ) [remainder]Correct:
foreach pid (0.016 ) cp lj.model fort.25 [remainder]
I ran this code for ideal gas bath pressures of 0.016, 0.032, 0.064,
0.128, 0.25, 0.50, 0.75, 1.0, 1.5, 2.0, 3.0, 4.0, 6.0, at a
temperature ![]() = 2.0 for 20,000 cycles and for
= 2.0 for 20,000 cycles and for ![]() = 108 particles
with an initial density of 0.6 (
= 108 particles
with an initial density of 0.6 (![]() = 180.0). The results are below:
= 180.0). The results are below:
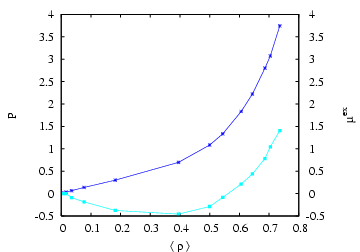 |
|
|