• Home
• Research
• Software
• Facilities
• People
• Publications
• Contact us

Network Coding (NC) is a communication paradigm for transferring and storing information in networks. The traditional approach to transferring information across networks is routing, where nodes in the network simply forward packets appearing on incoming links to other nodes via outgoing links. A network coding scheme allows nodes to combine the incoming packets via linear or non-linear functions and forward the result and outperforms routing in simplest of networks (e.g. see the celebrated butterfly network). Codes for distributed storage systems with certain repair and reliability requirements can be thought of as network coding schemes with the following objectives: 1) use as less storage space as possible 2) transfer as less information as possible during repair of failed nodes, all the while, satisfying the reliability requirements.

We study the limits on performance of network coding in a very general setting called multi-source multi-sink network coding over directed acyclic graphs (DAGs), which allows multiple senders and multiple receivers demanding to receive packets from arbitrary subsets of senders. The limits on performance of network coding for a given network are best described using its rate region which is the set containing all rate vectors for which communication is possible using some network coding scheme. Characterizing these sets using linear/non-linear inequalities is known to be a notoriously difficult problem in information theory. Yan et. al. [B1] provided the following implicit characterization of rate region R_*:

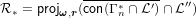(1)

where, ω is the vector of source information rates, r is the vector of edge capacities, Γ_n^* is the yet unknown 2ⁿ - 1-dimensional set of all entropic vectors, L′,L′′ are sets of constraints on entropy vectors encoding independence of sources and the fact that outgoing messages at a node are functions of incoming messages, and con(⋅),⋅,proj_ω,r(⋅) represent convex hull,closure and projection onto ω,r coordinates respectively.

Roughly speaking, R_* is the projection of a set with exponentially large dimension that is Γ_n^*. However, characterizing Γ_n^* is itself a long-standing fundamental open question in information theory. We use following approaches to handle this problem:

• Computation: Use computational means to determine rate regions of small networks. This is done by evaluating the formula in equation 1 with the unknown set Γ_n^* replaced by known bounds (strict subsets or supersets of Γ_n^*) on Γ_n^*. This is essential for providing intuition about large networks.
• Symmetry: Use symmetry of networks to gain insights into structure of rate regions and improving efficiency of algorithms for computing bounds on rate regions.
• Hierarchy: Develop a hierarchy of networks. Based on the lines of graph well quasi ordering, this approach revolves around different notions defining sub-networks (minor relations). We try answering questions like: For which classes of networks and minor relations can we determine rate regions of large networks using rate regions its subnetworks?
• Applications: We apply our computational tools to solve the data distributed storage systems. One of the earlier models on distributed storage systems is Multilevel Diversity Coding Systems (MDCS). We solved thousands of MDCS instances and investigate their sufficiency of simple codes and sufficiency of Shannon outer bound.

I Computation to determine the rate regions of small networks

Information theorists have traditionally proved rate regions by hand. This involves a converse proof: finding a collection of conic combinations of inequalities known to hold for the problem that gives the tightest collection of implied inequalities amongst all such collections, giving an outer bound on the rate region and an achievable code construction for every point in the outer bound, thus showing it to be the exact rate region. In network coding, however, this scheme falls apart due to sheer number of inequalities one must consider: e.g. the simplest polyhedral outer bound on Γ_n^*, the LP outer bound, has 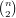2^n-2 + n inequalities[B2]. Imagine the manual labor required to find that many conic combination coefficients to prove just 1 inequality bounding the rate region! Similarly, finding an achievability scheme for a given rate point also involves a lot of head-scratching for arbitrary networks. Proving that a small network coding instance has a certain rate region can be seen as a three step process:

• Compute an outer bound R^out using outer bound Γ_n^out ⊃Γ_n^*
• Compute an inner bound Rⁱⁿ using an outer bound Γ_nⁱⁿ ⊂Γ_n^*
• Do they match?
  • Yes: Declare that we have found the rate region
  • No: Repeat step 1 and 2 with improved bounds

By improving the inner/outer bounds in step 3, we mean smaller outer bound Γ_n^out′ ⊂ Γ_n^out and/or a bigger inner bound Γ_n^in′ ⊃ Γ_nⁱⁿ. An important restriction we make when considering the inner/outer bounds in step 1) and 2) is to consider only polyhedral bounds that are in fact polyhedral cones. Steps 1) and 2) can now be stated as an instance of evaluating following equation,

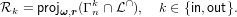(2)

where L is the intersection of all network coding constraints. This restriction allows us to use a variety of polyhedral computation algorithms for problems such as polyhedral extreme ray enumeration, redundancy removal, and projection, for which there are nice implementations out there (see cdd, lrs, chm). While most known polyhedral outer bounds on Γ_n^* have tractable inequality representations and humongous (mostly unknown) extreme ray representations, most polyhedral inner bounds are the opposite, with tractable extreme ray representations and humongous (mostly unknown) inequality representations.

I.1 Computing outer bounds

Outer bound R^out on network coding rate region can be obtained using an outer bound on region of entropic vectors Γ_n^out. If the outer bound used is Shannon outer bound of Γ_n, we get an outer bound R^LP on the rate region. Other outer bounds on region of entropic vectors, especially those tighter than Γ_n, can be obtained using non-Shannon outer bounds formed by adding non-Shannon information inequalities to Γ_n. One of the methods of computing non-Shannon information inequalities is by using Csirmaz’s extended copy lemma [B3]. Both of these problems: computation of of R^out and computation of non-Shannon information inequalities can be solved using our software chm that performs exact polyhedral projection using rational arithmetic and floating point simplex with basis identification for exact solutions to LPs (QsOpt_ex).

I.2 Computing Inner bounds

The most desirable property of an inner bound Γ_nⁱⁿ on region of entropic vector is a readily available construction of a collection random variables for every point in the bound. Two such classes of inner bounds are 1)Γ_n^q and 2)Γ_n,k,q^⊂space[A1], which are inner bounds obtained from 1) matroids representable over F_q 2) n-subspace arrangements over F_q that can be obtained from size k > n representable matroids. We device algorithms to compute these classes of inner bounds which are available in extreme ray representations of the associated polyhedral cones. Of special interest are the orderly generation algorithms [B4] and those based on homomorphism principle[B5].

I.3 From computer aided proof to traditional human-friendly proof

Recall that an inequality in the rate region of a network is in terms of rate variables (edge capacities) and source entropies. Sometimes, the inequalities in a rate region are easy to derive. However, for many instances, it is not easy to derive by hand all of the inequalities for the rate region. While we can use computation to find rate regions, when we are done, we would also like to have a more traditional converse proof i.e. we would like to know the conic combination of information inequalities that yielded a given rate region inequality. A technique based on LP duality is discussed in [B6, B7] using which we show how to use a computer to generate traditional converse proofs automatically.

The projection of the Shannon outer bound intersected with the network constraints gives an outer bound on the network coding rate region, which is in principle equivalent to a converse proof. Suppose a polyhedral cone P is determined by Ax ≥ 0. For an inequality implied by Ax ≥ 0, b^Tx ≥ 0, where b^T has zeros on eliminated dimensions, then there exists a vector λ ≥ 0 such that A^Tλ = b. The vector λ gives coefficients for the weighted sum of inequalities in P.

Such a coefficient vector λ need not be unique. Hence, among the various possibilities for λ satisfying b = A^Tλ, we want to select one that gives the simplest proof, which means it involves the smallest number of inequalities and constraints. This vector will thus be the sparsest vector λ, having the fewest non-zero entries, i.e. the lowest l₀-norm.

Because the l₀-norm is a complicated non-differentiable and non-linear function, this is a difficult optimization problem to solve directly. Hence we use the typical relaxation that replaces the l₀-norm with the l₁-norm. Furthermore, since λ ≥ 0, we do not need the absolute values in the l₁-norm, and the problem is approximated by the linear program

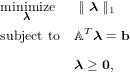(3)

which is equivalent to

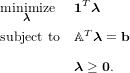(4)

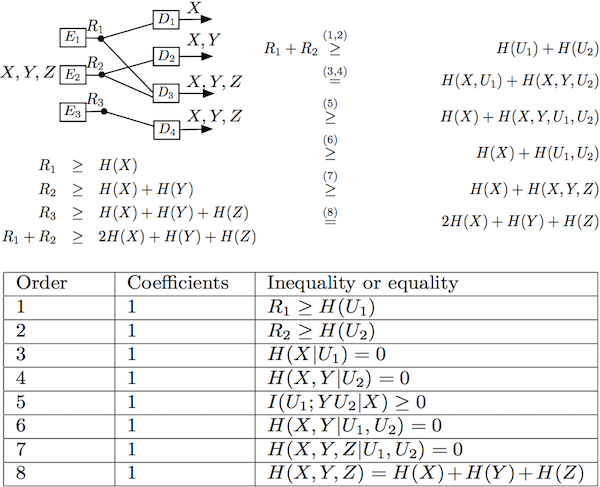
An example of the computer aided proof applied to an MDCS instance can be found in Fig. 1.

---

---

II Using of symmetry of networks to our advantage

Graph theoretic symmetry, symmetries of network codes, and symmetries of rate regions are inherently linked to each other.[A2] Network symmetry group (NSG) is the common thread between these notions of symmetry. It can be computed as a subgroup of the automorphism group of a directed cyclic graph appropriately constructed from the underlying network’s directed acyclic graph. Generalizations of Chen and Yeung’s partition symmetrical entropy functions [B8] can be obtained corresponding to any network symmetry group. Knowledge of the network symmetry group can be utilized to reduce the complexity of computing the LP outer bounds on network coding capacity as well as the complexity of polyhedral projection for computing frate regions. Symmetry can also be used for improving the efficiency of computing bounds on network coding rate region. For example, computing the LP outer bound R^LP [B2] on R^* is easier when the NSG is known. The algorithm that can compute R^LP when NSG is known is called symCHM [A3]. As the name suggests, it is a symmetry exploiting variant of CHM. symCHM is a general polyhedral projection algorithm i.e. it is not limited to computing network coding rate regions. Here is an example comparing symCHM to CHM.

---

---

III Hierarchy of Networks

On the lines of the the forbidden minor characterizations for combinatorial structures such as graphs and matroids, we would like to see if sufficiency of linear codes for networks also has forbidden network minor characterization, atleast for restricted classes of networks. We define embedding operations in such a manner that if a class of codes is not optimal for a small network, then all large networks that have this small network embedded in it will have the same property. Furthermore, since we can obtain a database of rate regions of small networks, we would like to extend the solvability to large networks. Thus, we defined some combination operations so that rate region of the large network can be obtained from the rate regions of small networks involved in the combination.

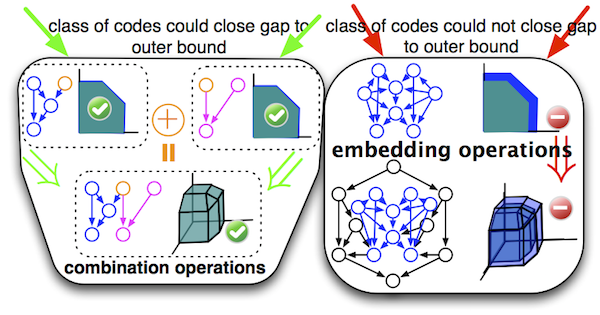
Fig. 3: Network embedding and combination operations to preserve important properties.

A demonstration of usefulness of embedding operations can be found in [A4], where we obtained forbidden minor list for MDCS problems up to 3-level 4-encoders ,with respect to the following properties 1) Sufficiency of binary scalar codes for achieving the entire rate region 2) Sufficiency of superposition coding, as in Fig. 4.

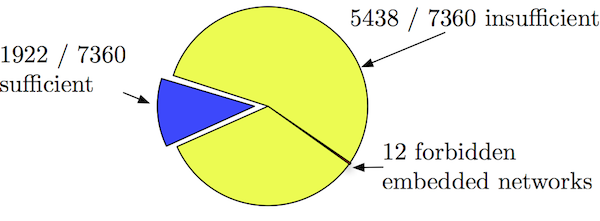
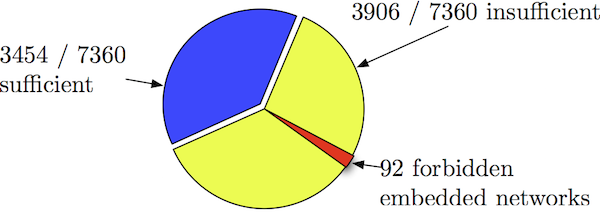
Fig. 4: Forbidden network minors for scalar binary codes (upper) and superposition coding (lower) on MDCS problems.

As a demonstration of usefulness of combination operations is shown in Fig. 5, which shows how to solve a large network by using combination operators on some small networks and their rate regions.

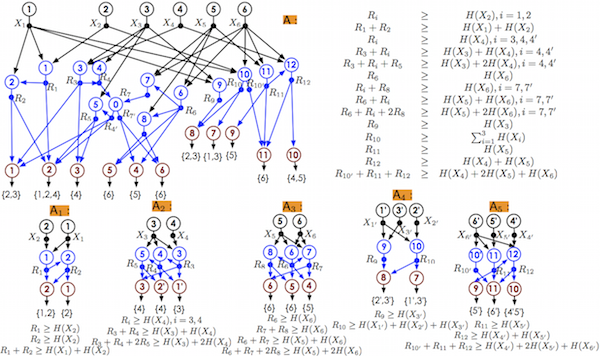
Fig. 5: An example of large network that is a combination of five small networks and it can be solvable by combining rate regions of the five small networks. We have further extended these operators to general hyperedge networks in [A5]. We show that by applying recursively the seemingly straightforward combination and embedding operators described above, one can reason about large networks using small networks that are not directly related to them via one-shot use of combination and/or embedding operators.

Funding for this Topic:

This work supported by the National Science Foundation under CCF-1421828 and CCF-1016588.

Relevant Publications & Presentations

External References