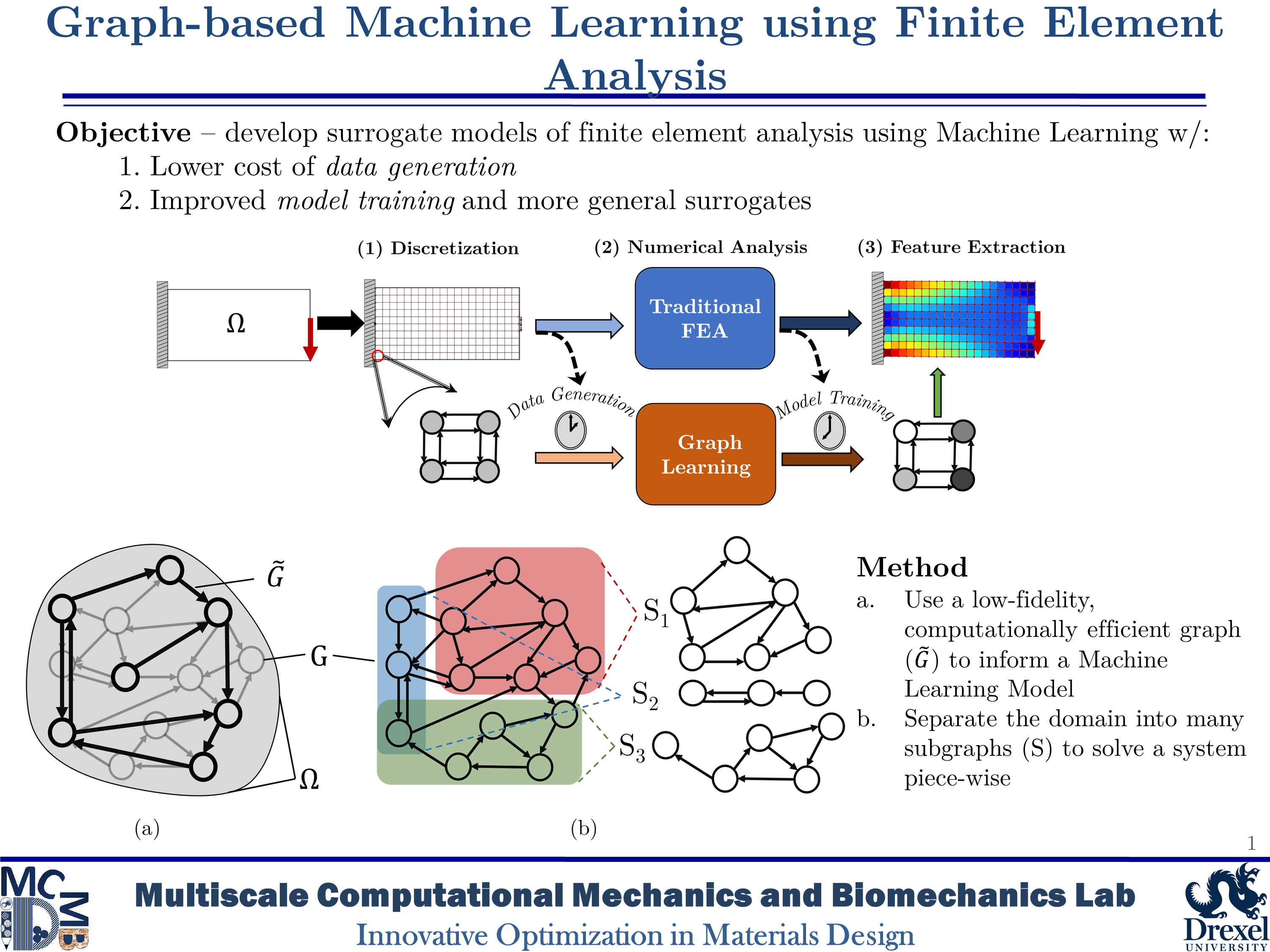
We are investigating machine learning techniques as viable alternatives to traditional physics-based modeling and partial differential equation solvers. Compared to more common applications of machine learning like natural language processing and image classification, physics-based machine learning faces some unique challenges. Namely, these challenges include (1) excessive data generation costs in developing training datasets and (2) increased accuracy and reliability requirements.
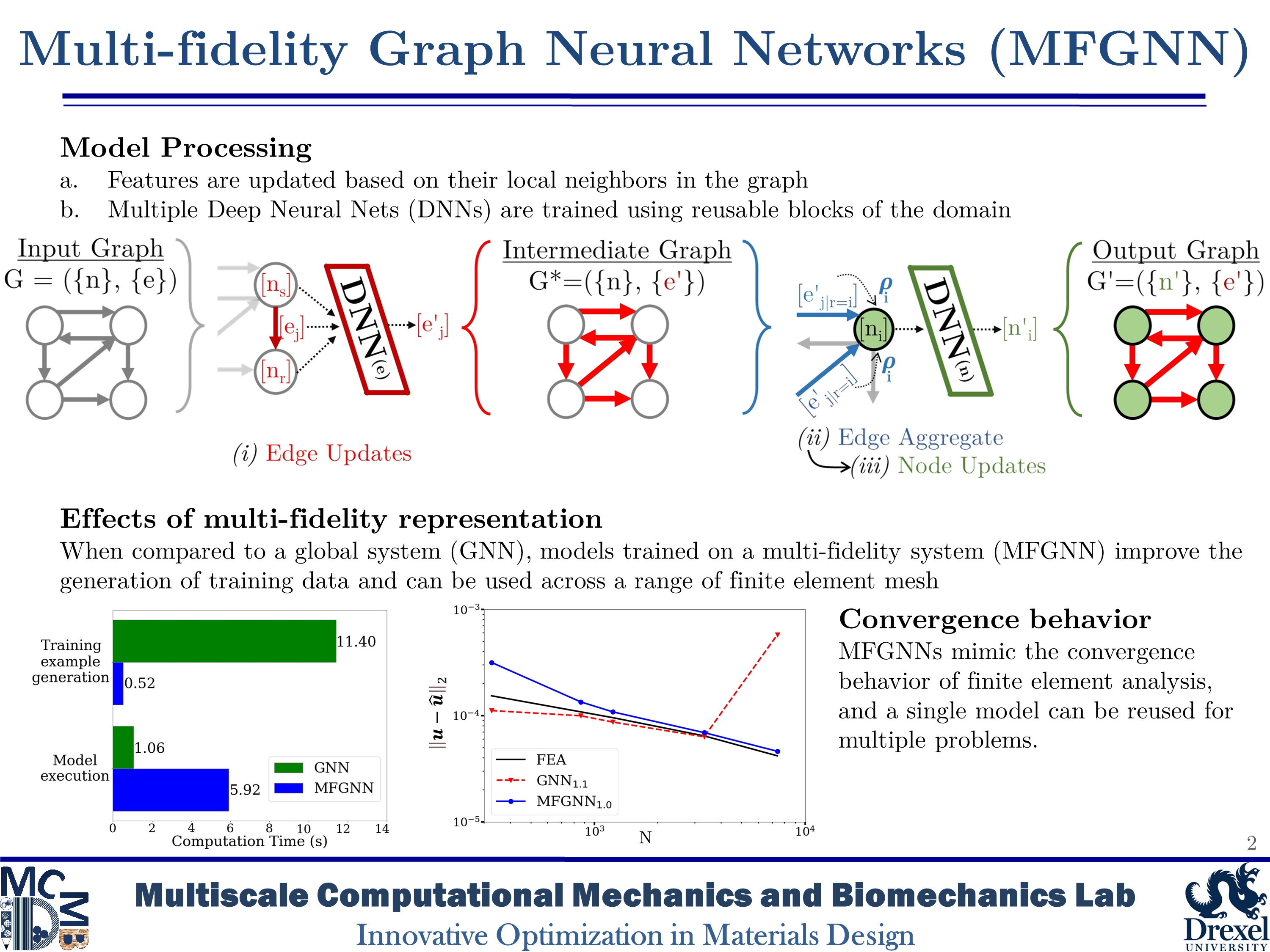
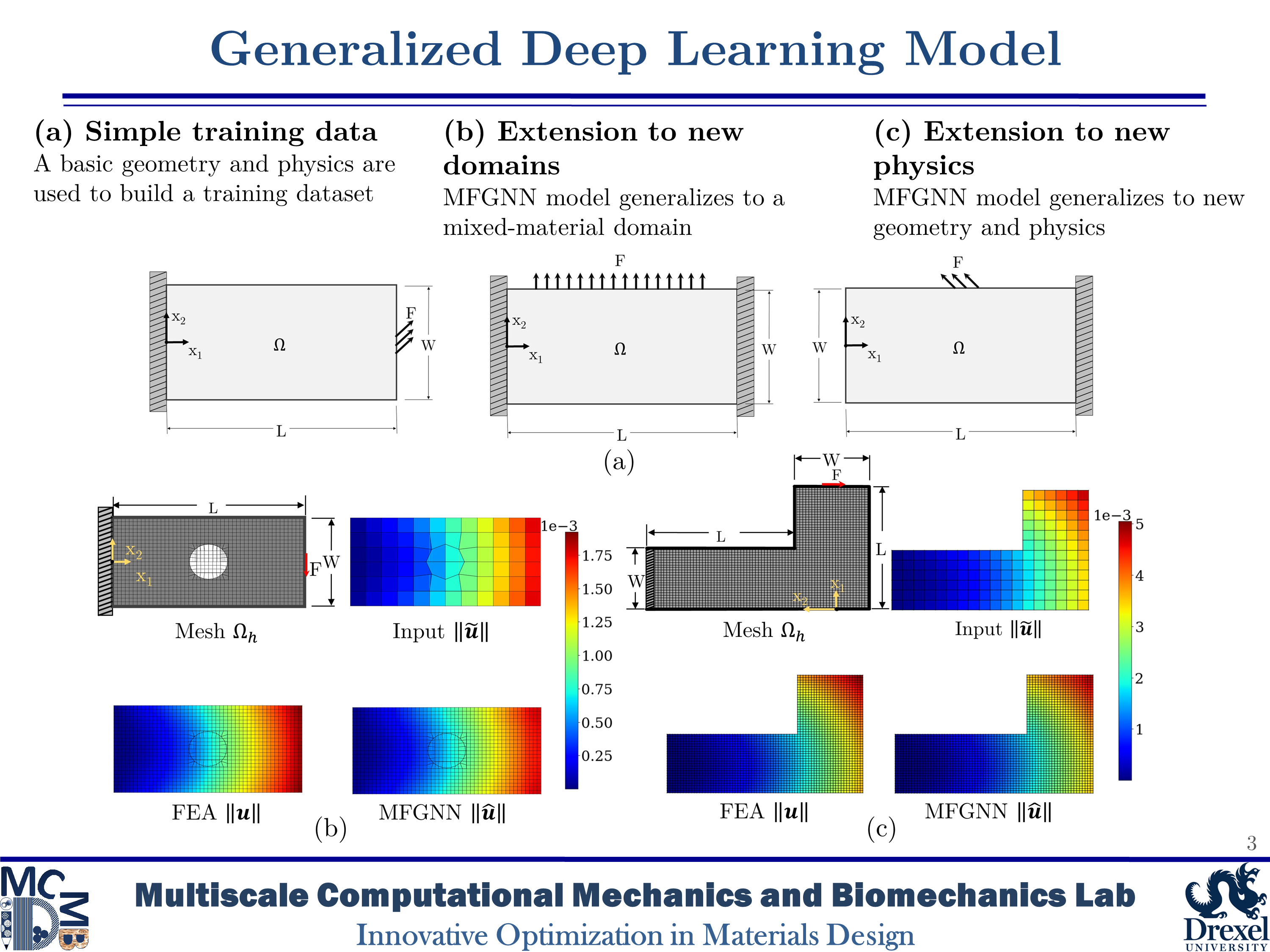
To meet these challenges, we have investigated graph-based machine learning. Our first work in this field introduces the Multi-fidelity Graph Neural Network (MFGNN). The MFGNN uses multi-fidelity data and subdomain analysis to reduce training costs, improve accuracy, and increase model generality.
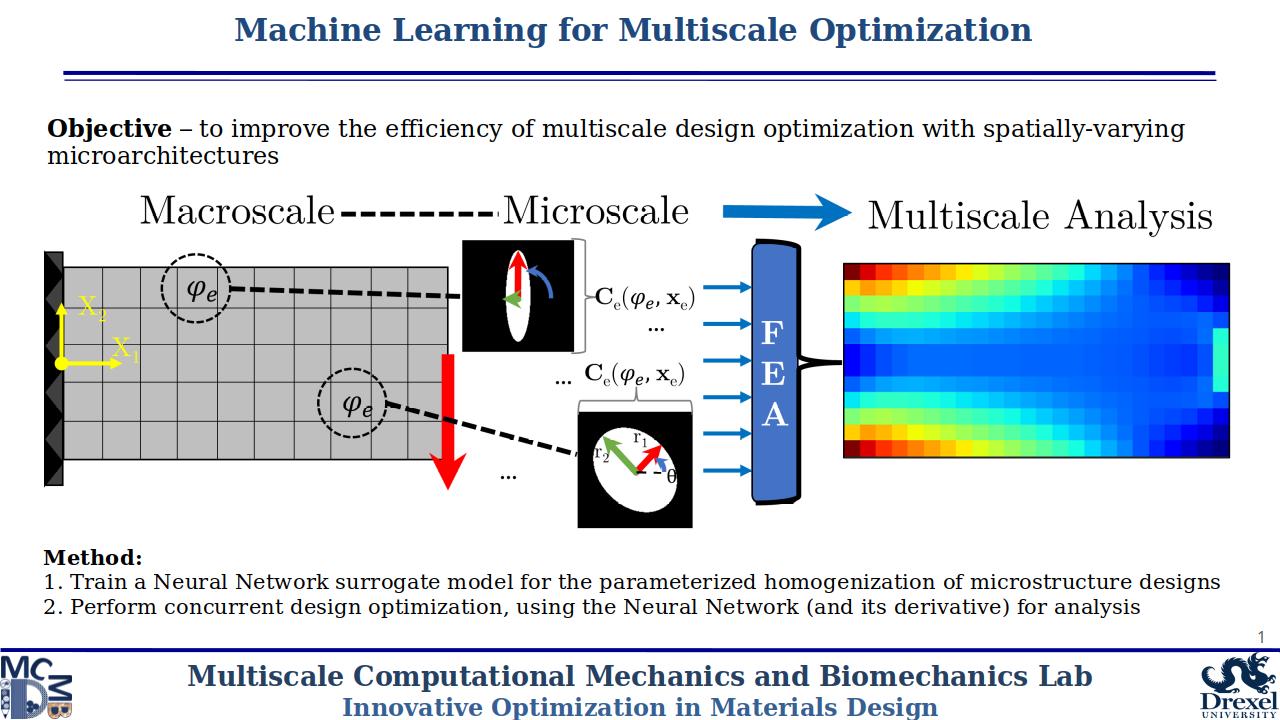
Multiscale design optimization is a notoriously computationally expensive process, requiring nested analysis schemes across multiple physical scales. We are investigating machine learning techniques to improve these processes and design structures with spatially varying microarchitectures that incorporate multiscale and multifunctional effects.
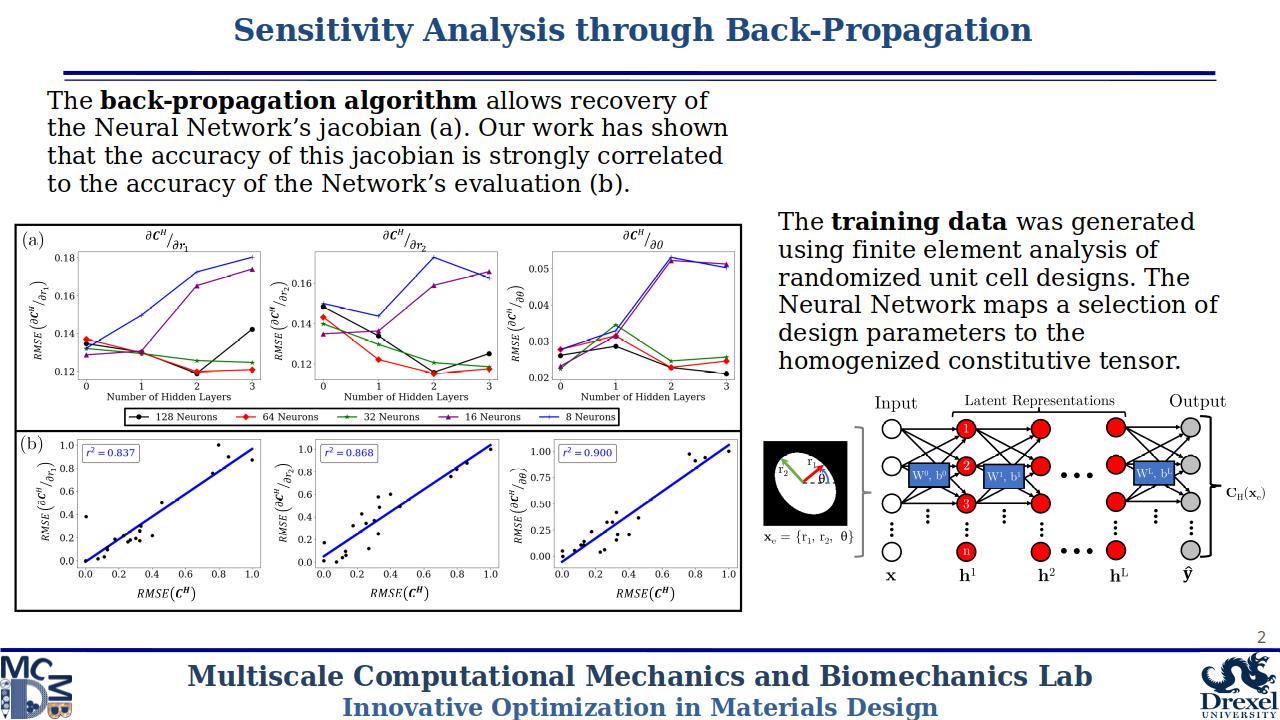
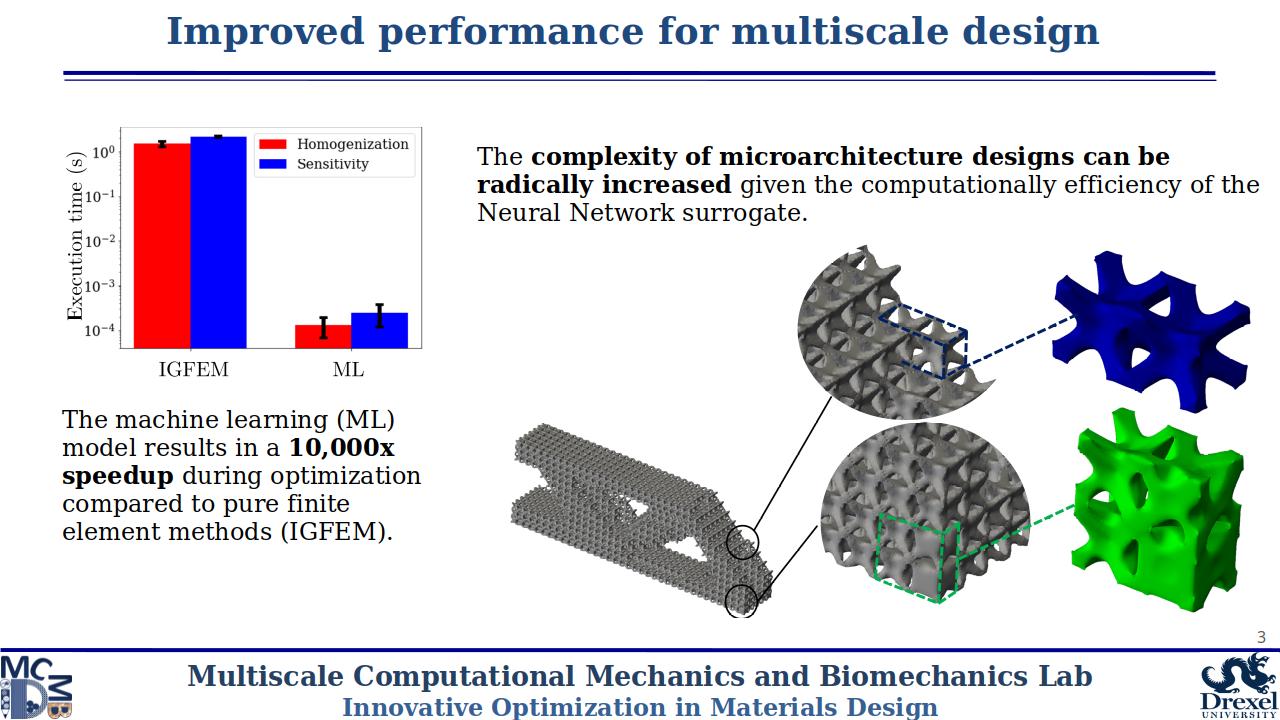
Our first work in this area considers the concurrent design of spatially varying microarchitectures for structural optimization. We employ a system of Neural Networks to approximated the effective constitutive relation of parameterized microstructures. Through backpropagation of the Neural Network, sensitivity information is efficiently recovered, resulting in 1,000-10,000x speedups of the concurrent design process.
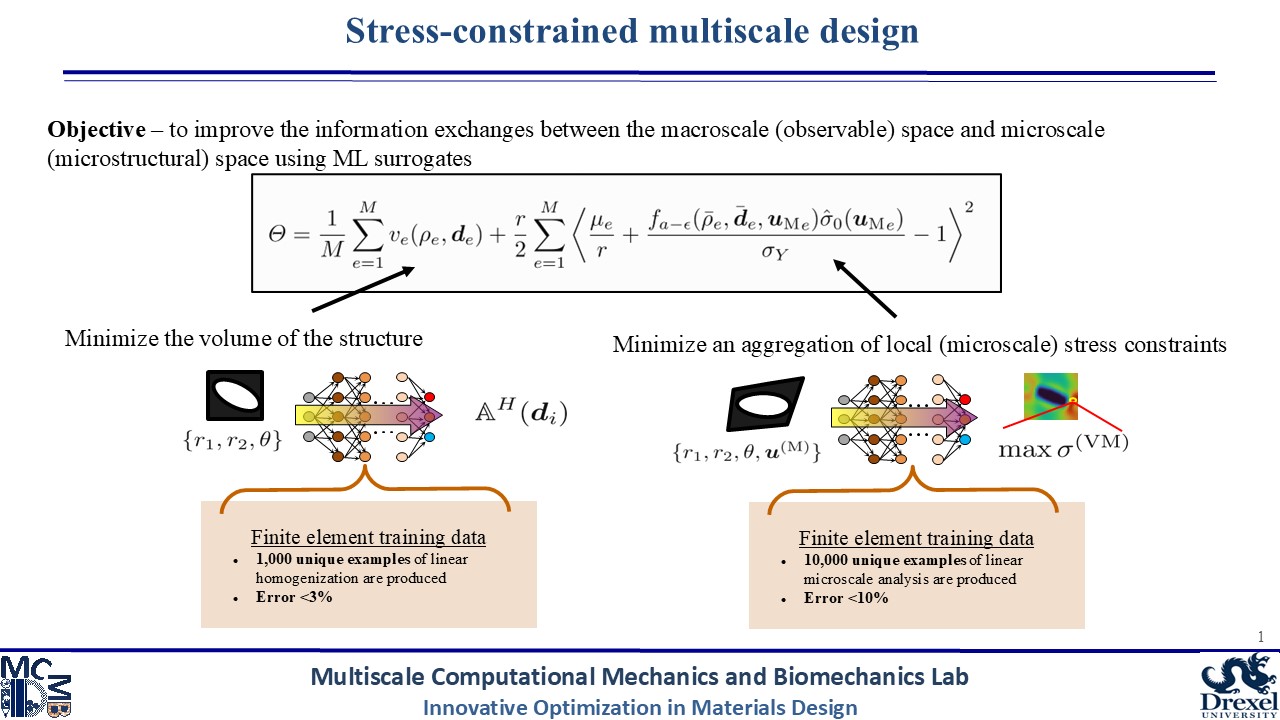
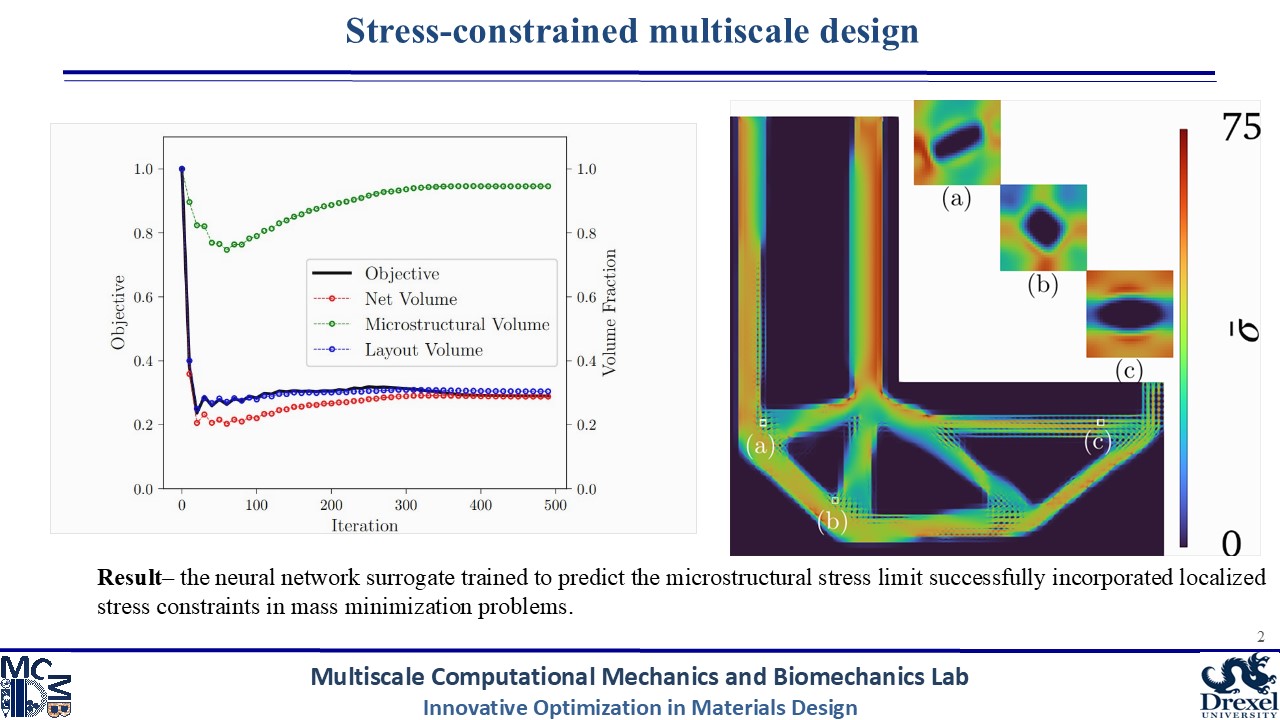
Machine learning surrogates also enable extension of the multiscale design space. We have applied a system of neural networks to not only homogenize microstructure designs, but also predict the maximum localized stress within each microstructure. Through prediction of this localized stress, we are able to perform stress-constrained design of multiscale structures. Performance gains are achieved by performing finite element analysis only on the macroscale/homogenized domain; the fast and efficient neural network surrogates deal with all the microscale analysis, including the prediction of localized stresses. Therefore, we are able to define stress constraints based on fine scale features without expensive computational modeling.
Related Publications
-
- Black, N. and Najafi, A.R., “Learning finite element convergence with the Multi-fidelity Graph Neural Network”, Computer Methods in Applied Mechanics and Engineering, vol 397, 115120, 2022.
- Black, N. and Najafi, A.R., “Deep neural networks for parameterized homogenization in concurrent multiscale structural optimization”, Structural and Multidisciplinary Optimization, 66, 20 (2023). https://doi.org/10.1007/s00158-022-03471-y
- Black, N. and Najafi, A.R., “Stress-constrained optimization of multiscale structures with parameterized microarchitectures using machine learning”, Structural and Multidisciplinary Optimization, 67, 102 (2024). https://doi.org/10.1007/s00158-022-03471-y
