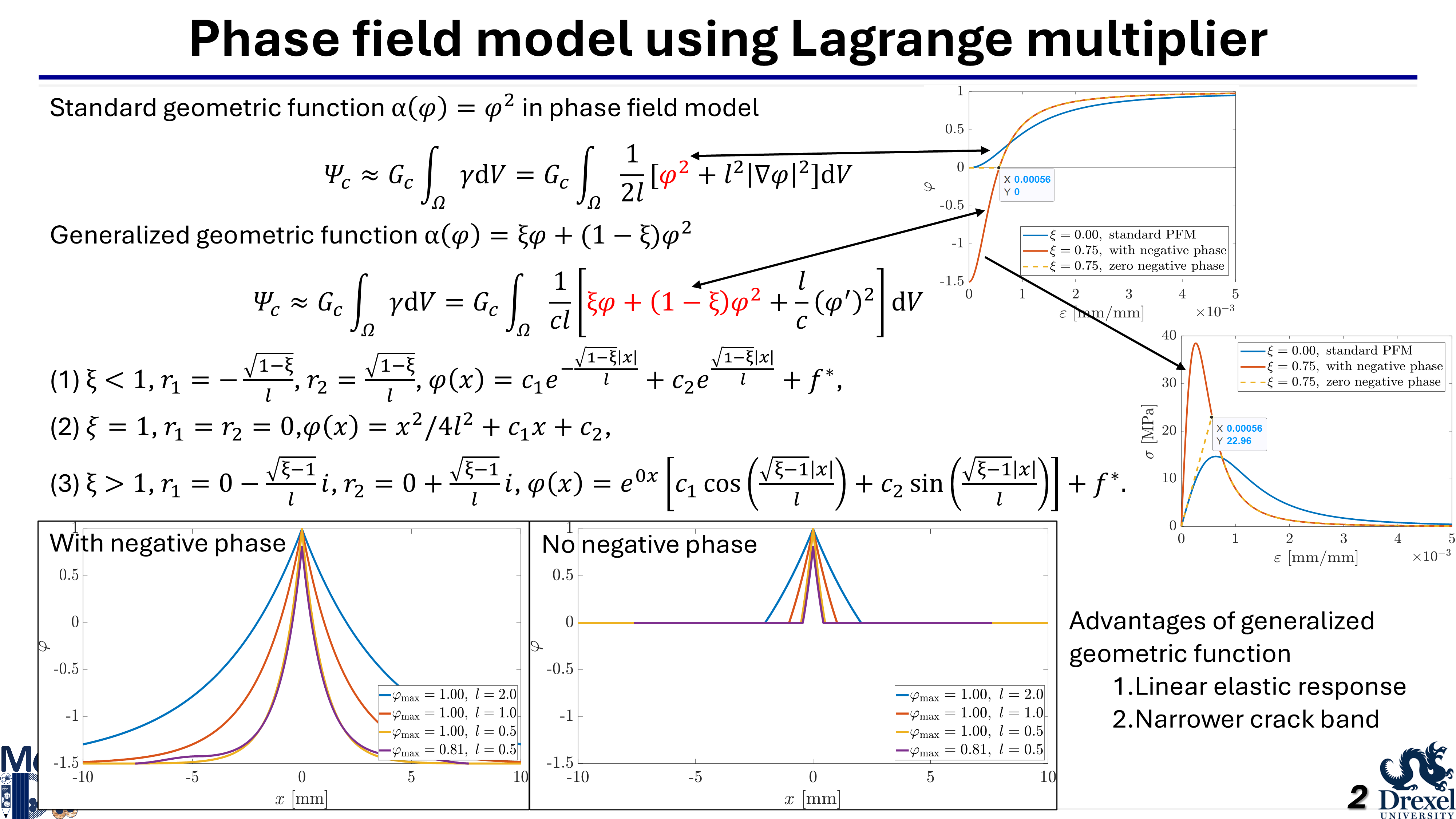
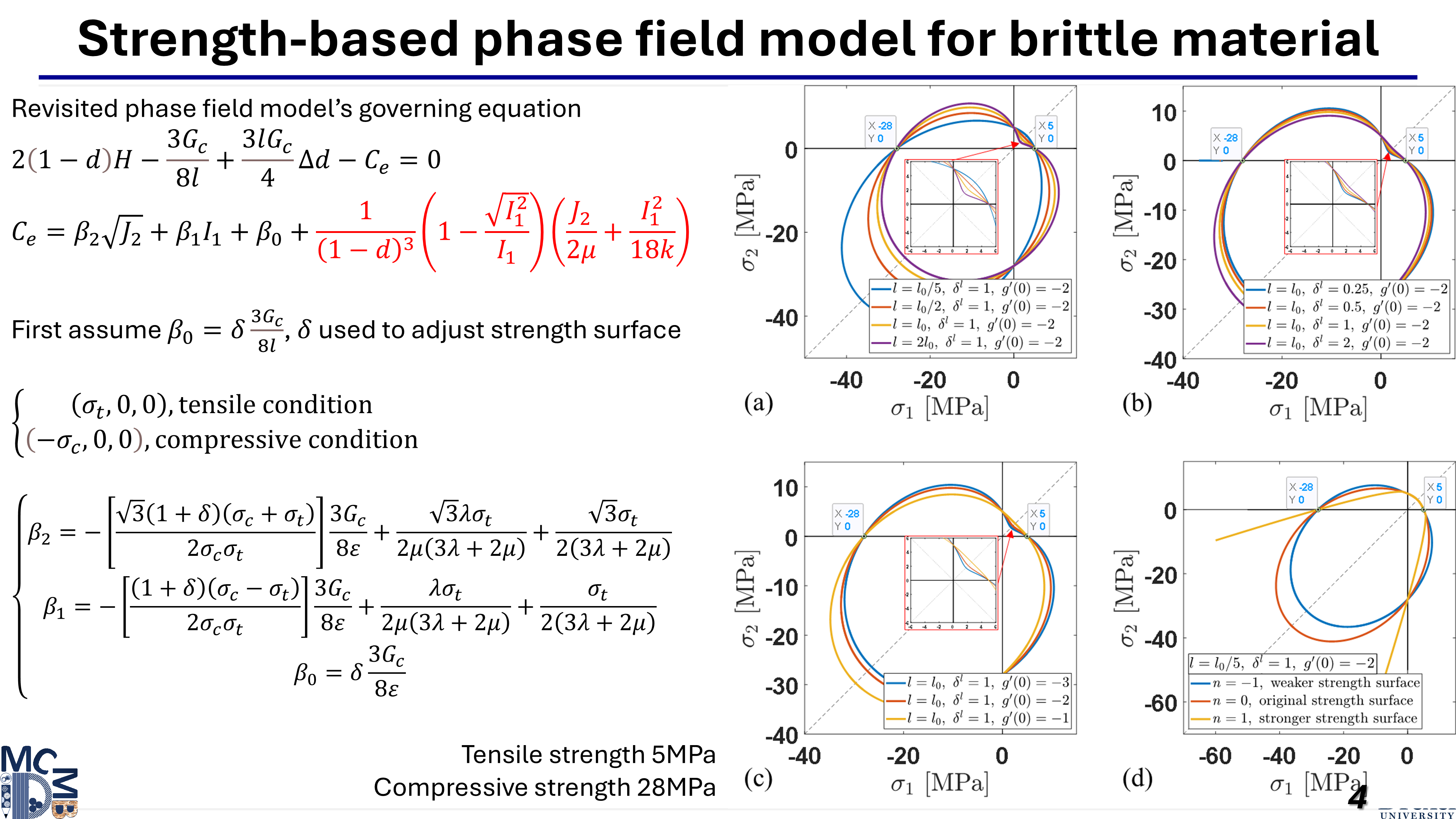
The classical phase field model for brittle fracture, based on a second-order geometric degradation function (known as the AT2 model), uses a phase field variable ranging from zero to one to represent material damage. Although widely applied in static and dynamic fracture scenarios, this model introduces artificial nonlinearity and inelasticity in the stress–strain response. An alternative approach, the AT1 model, employs a linear degradation function and produces a stress–strain curve with a clear linear elastic threshold. However, both AT1 and AT2 models are sensitive to the length scale parameter, making it difficult to simultaneously control fracture strength and the width of the regularized crack zone.
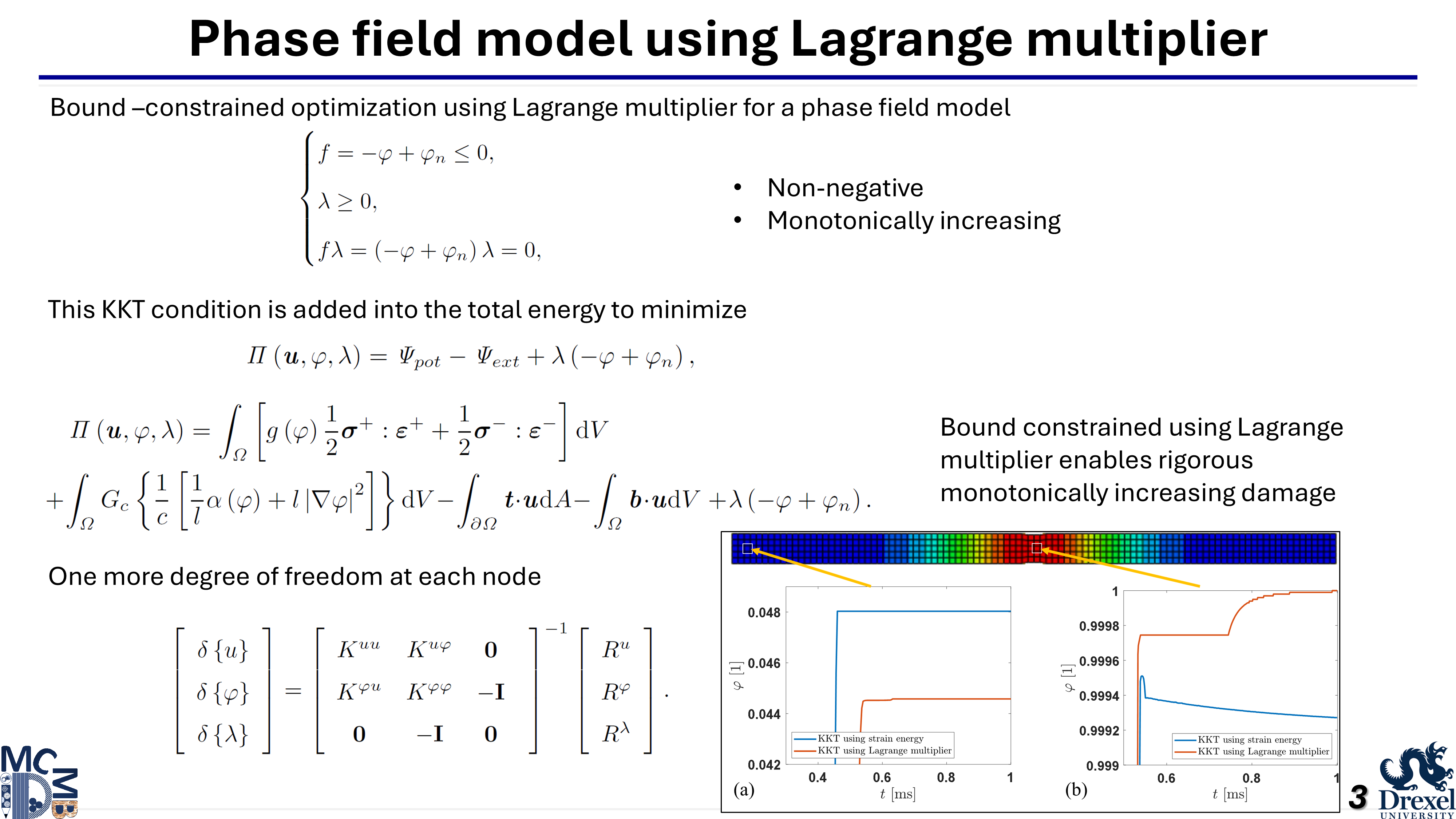
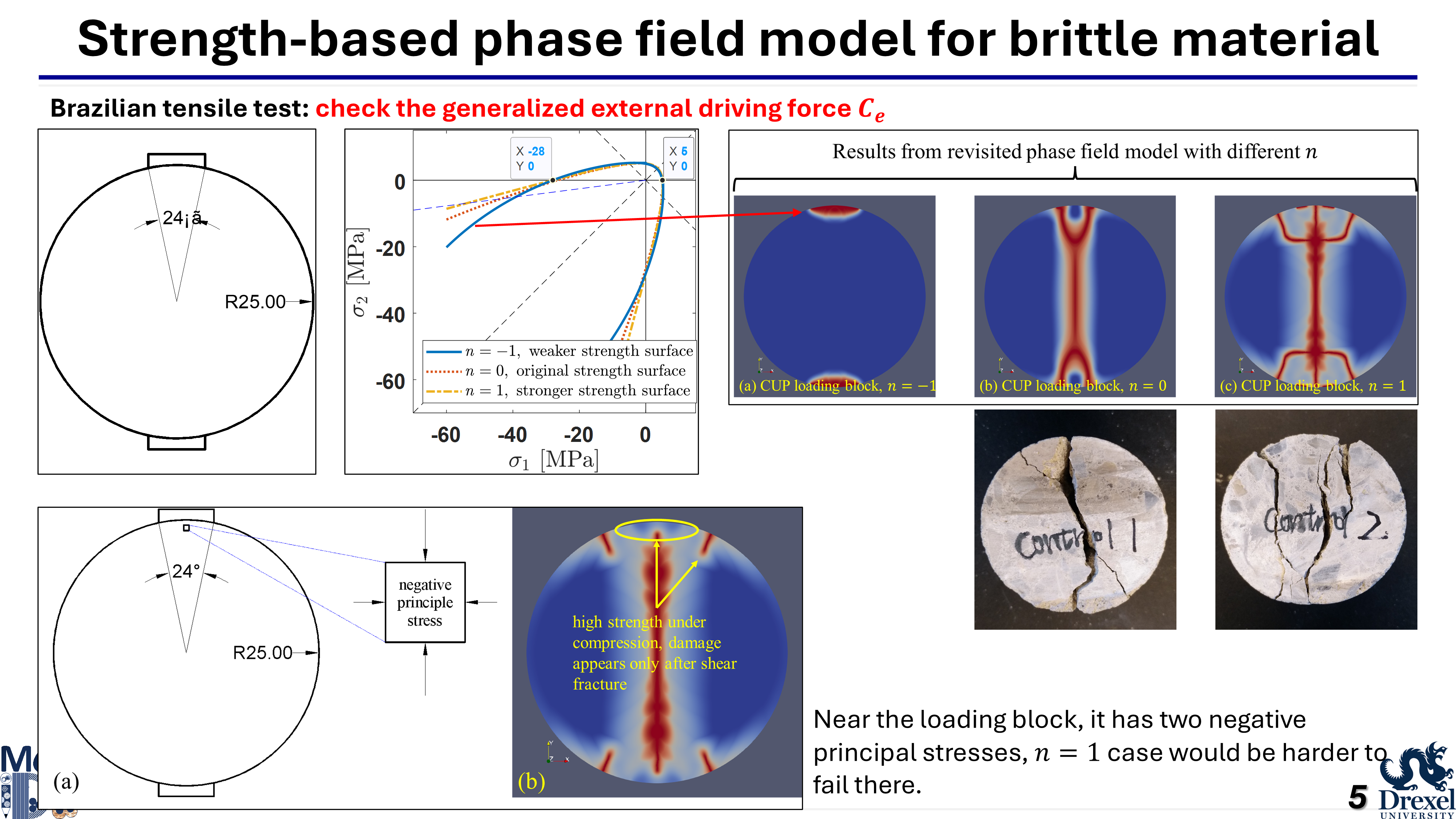
This work proposes a generalized quadratic degradation function that blends features of the AT1 and AT2 models, introducing an additional parameter to eliminate length scale sensitivity. Despite this advantage, the model may still produce non-physical negative phase values. To address this, a bound-constrained optimization approach is developed using Lagrange multipliers, allowing the enforcement of irreversibility and non-negativity directly on the phase field variable. The Karush–Kuhn–Tucker conditions are reformulated accordingly. The model is validated through several simulations, including single-element tests, cyclic loading in a bar, a Mode I Brazilian test compared with experimental data, and additional Mode II and mixed-mode tests benchmarked against published results.

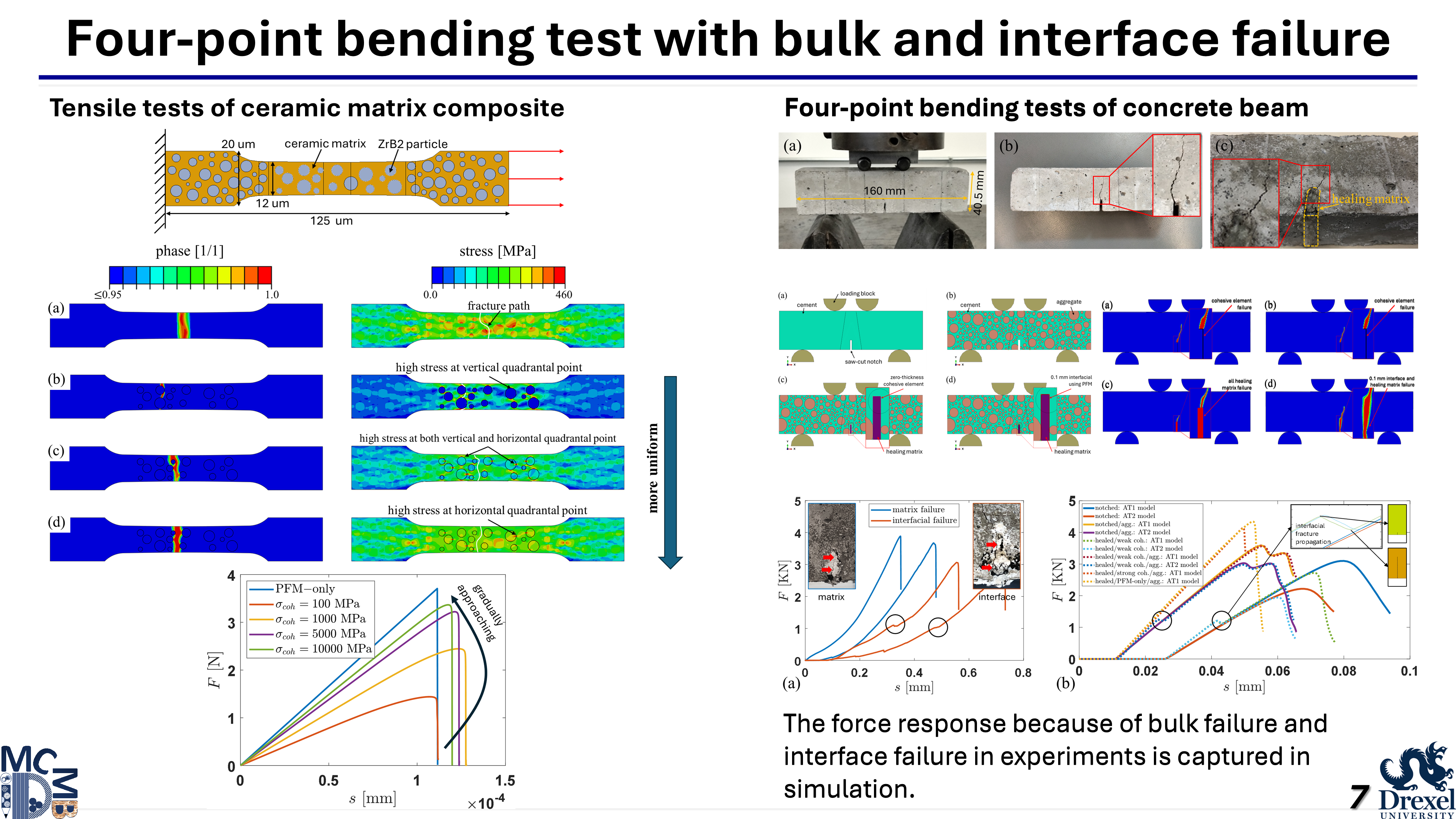
Related Publications
Meng, L., Lee, H. W., Ashkpour, A., Sales, C. M., Farnam, Y. A., Hubler, M. H., & Najafi, A. R. (2024). Bound-constrained optimization using Lagrange multiplier for a length scale insensitive phase field fracture model. Engineering Fracture Mechanics, 310, 110496.
